A Simple Definition of Probability Theory
Imagine that a street performer invites you to play a game: you need to guess the total of the 2 rolled dice to win a prize. It’s impossible to predict which total from 2 to 12 will be on the dice. But if you say 7, you’ll have a better chance of winning than if you say 2. This is what probability theory is about.
At 5-Minute Crafts, we would like to explain, in simple terms, what probability theory is.
What is probability theory?
Let’s make the situation with the dice simpler by using an ordinary coin. If you flip it, you’ll either get heads or tails. Try flipping the coin 100 times and you’ll see that each side of the coin comes up about the same number of times. It means the probability of flipping either heads or tails is 50%.

If you roll the dice, you’ll get a total from 2 to 12 (according to the numbers on the sides of the dice). The total number rolled on the dice will be a random variable. In other words, a random variable is a numerical expression of the result of a random event.
If you flip a coin, you get either heads or tails. These are 2 random events. Each of them may or may not happen. An event is a basic element of probability theory.
Probability theory is the branch of mathematics that studies patterns associated with random phenomena: random events, random variables, their properties, and operations on them.
What’s sample space?
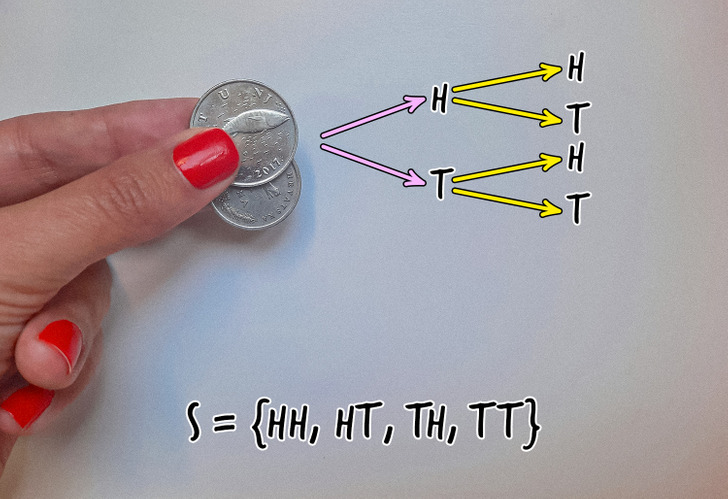
Let’s take 2 coins. If you flip each of them, you’ll get heads or tails, 1 of 2 possible events. And how many possible events can you get if you flip 2 coins at the same time?
Let’s take a look at the picture above. The letter T stands for when you get tails, and the letter H stands for the event when you get heads. Let’s say that when you flip the coins for the first time, you get heads on one coin and tails on the other. When you flip the coins for the second time, each coin can show either heads or tails, which will eventually give you 4 possible combinations based on the outcome of 2 flips. The thing that you see in the picture is called a tree diagram. It depicts all possible independent events in the given series.
So the combinations of HH, HT, TH, and TT represent all the different outcomes of our series and are called a sample space, which is denoted by the label S.
How to find probability with a formula
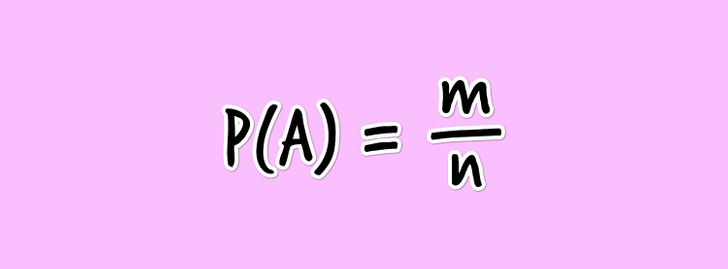
The probability that an event will or will not happen in a particular series can be calculated using the formula, P(A) = m/n, where “P” is the probability of the event, “A” is the event, “n” is the total number of all possible outcomes of this series, and “m” is the number of outcomes due to which event “A” can happen.

Let’s take candies of different colors as an example. There are 51 candies in the package, 6 of which are blue. The probability that you will get a blue candy from this package (event A in this case) is: P(A) = m/n. It means 6/51, or a little more than 11% (instead of using a fraction, we can write the probability as a percentage).
- If all candies in the package are blue, then the probability that you will get a blue candy will be 51/51 = 1.
- If you want to find the probability of getting a purple candy from this package, you will get 0/51 = 0.
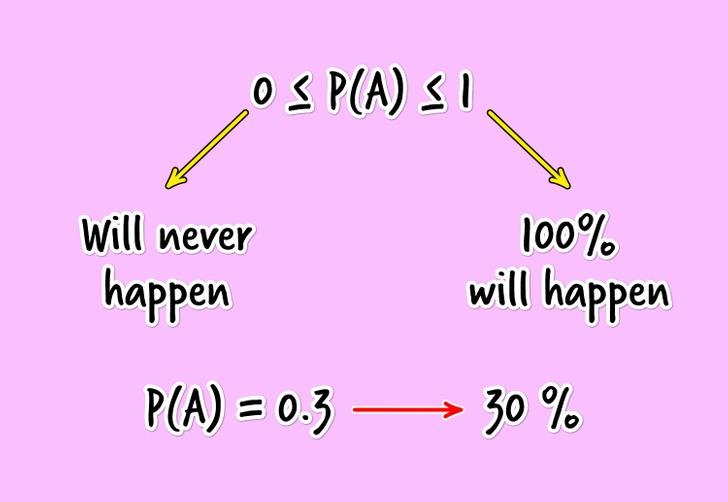
Based on the above, we now know that probability has a few properties:
- If the probability of an event is 1, then it will 100% happen.
- If the probability of an event is 0, then it will never happen.
- Between 0 and 1, there is a positive number that shows the probability of a particular random event. If the probability of an event is 0.3, this means that it will happen with a probability of 30%.
Taking this into account, we can conclude that the probability of any event is 0 ≤ P(A) ≤ 1.
How to solve easy probability practice problems
Problem 1: There are 15 apples in the basket — 10 of them are green and 5 are red. What is the probability of getting a yellow apple from the basket?
Solution: Let’s use the formula, P(A) = m/n. In this case, n = 15 and m = 0. Therefore, the probability of getting a yellow apple out of the basket is P(A) = 0/15 = 0. In other words, it’s impossible.
Problem 2: There are 36 cards in the deck. You take one card out of it. What is the probability that this is a card of spades?
Solution: Let’s use the formula, P(A) = m/n. In this case, n = 36, and m = 9 (that’s how many cards of spades are in the entire deck). This means that the probability of the desired outcome is equal to P(A) = 9/36 = 0.25, or 25% probability that you will get a card of spades.
Addition and multiplication theorems of probability

Imagine that you have 3 piles in front of you, and each has 10 pieces of a construction toy. The first pile has 8 pieces for building a house, the second pile has 7 pieces, and the third one has 9 pieces. All other pieces are decorative elements and parts of mini-figures. You pick one random piece from each pile. What is the probability that all 3 pieces you’ve picked will be building pieces?
Let’s specify the conditions: If you take a building piece from one pile, this doesn’t mean that you will or will not get a similar piece from the other 2. In other words, these events are independent of each other (the probability of the occurrence of any of them doesn’t depend on the other events).
So, we can consider 3 independent events. Let’s find the probability of getting a building piece for each pile:
- First pile: 8/10, or 0.8, or 80%
- Second pile: 7/10, or 0.7, or 70%
- Third pile: 9/10, or 0.9, or 90%
To find the probability of simultaneous occurrence of these 3 independent events, we need to multiply them: 0.8 × 0.7 × 0.9 = 0.504. So the probability that all 3 pieces will be building pieces is 0.504, or more than 50%.

We solved this problem using the multiplication theorem of probability, which looks like this:
P(A × B) = P(A) × P(B|A)
The formula means that the probability of the product of 2 events is equal to the product of the probability of one of them, and the conditional probability of the other is calculated under the condition that the first event occurred (the part of the formula written as P (B|A) denotes the probability of event B, provided that event A happened). Wherein:
- Event A is independent of event B if the probability of event A doesn’t depend on whether event B occurred or not.
- Event A is dependent on event B if the probability of event A changes depending on whether event B occurred or not.
If we are dealing with independent events, then the formula looks like this:
P(A × B) = P(A) × P(B)

Problem: There are balls in a bowl — 2 of them are orange and 3 are blue. You take 2 balls out of the bowl simultaneously. What is the probability that both balls are orange?
Solution: Let’s consider the simultaneous extraction of 2 orange balls to be “event A.” It will be the product of 2 events: A = A1 × A2, where:
A1 is an orange ball taken out of the bowl during the first attempt.
A2 is an orange ball taken out of the bowl during the second attempt.
P(A1) = 2/5
P(A2) = (2-1) / (5-1) = 1/4
P(A) = P(A1 × A2) = 2/5 × 1/4 = 0.1. Therefore, the probability that both balls will be orange is only 0.1, or 10%.
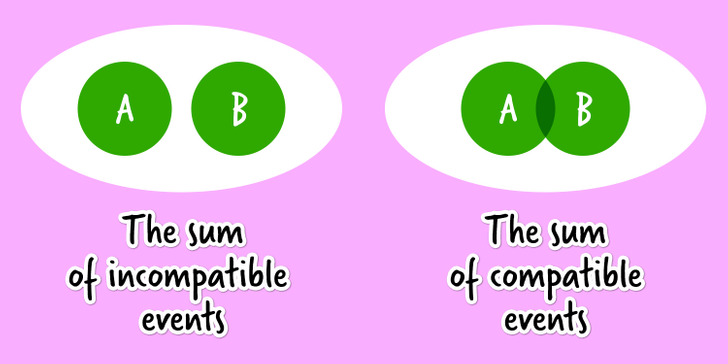
The sum of 2 events A and B is event A + B, at which either event A, event B, or both events will occur simultaneously. If the events are incompatible (meaning the occurrence of one event excludes the occurrence of the other within the same series), then either event A or event B may occur.
By flipping a coin, we get 2 opposite and mutually exclusive events: you may get either heads or tails. When 2 events are opposite to each other, they are indicated by the same letters, but a dash or an apostrophe is added above one of them. For example, it would be A and Ā or A and A’.
Imagine that you have 9 pears in a bag of fruit — 4 of them are green, 3 are red, and 2 are yellow. You take one of them at random. What is the probability that it is not yellow?
To answer the question, you need to find the probability that you will get a green pear (A) and a red one (B), and then add them together (A + B) to find the probability that you will get one or the other (but not yellow).
P(A) = 4/9
P(B) = 3/9 = 1/3
These 2 events are incompatible. Let’s add their probabilities together:
P(A+B) = P(A) + P(B) = 4/9 + 1/3 = 7/9.
So the probability that the pear you’ve taken is not yellow is 7/9, or more than 77%.

To solve this problem, we used the formula, P (A + B) = P (A) + P (B), from the probability addition theorem, meaning, “The probability of occurrence of 1 of 2 incompatible events is equal to the sum of the probabilities of these events.”
If we are dealing with compatible events (meaning the occurrence of one event doesn’t exclude the occurrence of the other one within the same test), the probability of their sum is calculated by the formula: P(A + B) = P(A) + P(B) − P(A×B).
These formulas can be used to solve simple probability problems.
Bonus: what “a chance of rain” in a weather forecast really means

Imagine that tomorrow’s weather forecast says there is a 30% chance of rain. This figure seems insignificant. So the following day, you go for a walk around the city without an umbrella and end up getting soaked. How could this happen if they said that there was only a 30% chance of rain?
If the chance of rain mentioned in the weather forecast for your city is 30%, this indicates a 100% chance of rain, but it will only happen in 30% of the area. If you move around the city on this day, then you will increase your chances of getting wet.
