Order of Operations in Math, and Why People Get Confused Without It
All of us have known about the order of operations in math since school. However, we tend to forget these rules, and because of this, we can make mistakes in everyday calculations.
5-Minute Crafts would like to explain what the order of operations in math is about, why even adults can make mistakes while solving simple math problems, and why it is important to know it at any age.
Why is it important to follow the order of operations?
The basic arithmetic operations in math are:
- addition (+)
- subtraction (-)
- multiplication (×)
- division (÷)
If a single operation is used in a numerical expression, it won’t be difficult to solve this math problem. For example, 3 + 2 = 5 or 6 ÷ 3 = 2. If there are 2 or more operations, you need to perform actions in a certain order to get a correct answer.

There are 3 math problems above, and it’s easy to get the wrong result while solving each of them if you forget about the correct order of operations in math. Try to solve these problems yourself, and then compare your results with the correct answers at the end of the article. If you solve at least one of them incorrectly, perhaps you should try again to remember the rules regarding the order of operations with us.
Rule 1: Operations should be performed one-by-one from left to right.

✅ While performing basic arithmetic operations, you need to go left to right.
Look at the picture above. To calculate the result of the expression 6 ÷ 3 × 2, it is necessary to perform operations one-by-one from left to right, first dividing 6 by 3, and then multiplying the result by 2. If you perform the operations in a different order (first multiplication, and then division), you’ll get the wrong result.
❗ If an expression only consists of multiplication or addition operations, then, according to the сommutative property, the result of the expression doesn’t depend on the order in which the operations are performed.
Rule 2: Multiplication and division go first, followed by addition and subtraction.

A mathematical expression can have several different arithmetic operations, as shown in the picture above. Let’s write this expression down as 2 + 2 × 2. If we perform all the operations one by one from left to right, we’ll get 2 + 2 × 2 = 4 × 2 = 8. This result is wrong (this can be proved by simple counting of the unit squares in the photo). So why is it wrong?
✅ We’ve described 4 basic arithmetic operations above. They are not equal in priority, which affects the order in which you need to solve the problem. Multiplication and division have priority over addition and subtraction. If an operation has a higher priority, then it should be performed first.
Let’s put this into practice and solve the problem again: 2 + 2 × 2 = 2 + 4 = 6. This answer is correct.

❗ If there are 2 or more equivalent operations in the expression, they should be performed one-by-one from left to right. Thus, multiplication and division are equivalent operations and the order in which they are performed depends only on the place they appear in the expression. The same goes for addition and subtraction.
Above is an example of solving the expression 12 ÷ 3 × 6 — 12 ÷ 6 × 3. According to the rules, you need to perform division and multiplication first, going left to right, then division and multiplication again on the right end of the expression, and you don’t need to perform subtraction until the very end. If the order is broken, the result will be wrong.
Rule 3: Exponents and square roots should be performed before other operations.
✅ If the expression has a number that needs to be raised to a power or you need to do the inverse operation (solve for the square root), this needs to be done before performing basic arithmetic operations.
For example, let’s try to solve what 4 + 2 +22 + 32 is equal to. To do this, you need to alternately raise 3 and 2 to the second power, getting 4 + 2 + 4 + 9, and then sum up all the numbers and get 19 as the result.
❌ It’s easy to make a mistake here by adding the numbers with the same exponents (that is, 22 and 32) together, and then raising the resulting sum to a power.
Rule 4: The operations in parenthesis are always performed first.

✅ If part of the expression is inside parenthesis, it must be solved first. Then go exponents and square roots, then you can perform the rest of the operations, respecting the priority and going left to right.
The picture above shows a simple math problem. The solving process on the left follows the correct order of operations: first we get the result in brackets, then we perform multiplication operations from left to right, and at the end we do the addition operation. The solving process on the right is wrong, because all operations are performed from left to right without following the proper order, and the result is also wrong.

✅ The operations in parenthesis should be performed from left to right and according to the rules of priority.
In long expressions, you can put numbers above the operations to show the order in which the operations should be performed, as shown in the example above. This makes the solving process easier.
How to memorize the order of operations
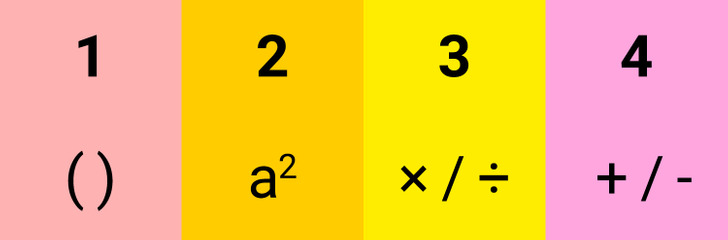
1. If there are parenthesis in the expression, do the things inside them first.
2. If you need to solve for exponents or square roots in the expression, do this before performing other operations.
3 and 4. Among the 4 basic arithmetic operations, multiplication and division have a priority over addition and subtraction, so they are performed first. Operations of equal priority are performed one after another from left to right.
The answers to the math problems at the beginning of the article
- 8 ÷ 4 × 2 = 2 × 2 = 4
This is a rather simple problem. It’s unlikely you made a mistake here, since you solved it by simply performing operations one after another, going left to right.
- 6 ÷ 2(1 + 3) = ?
This problem looks simple, but it can baffle even math professors. This is because you can get different results depending on how you solve it. For example, you can solve it like this: 6 ÷ 2(1 + 3) = 6 ÷ 2(4) = 3 * 4 = 12. But if you rely on the distributive property (where a(b + c) equals a × b + a × c ), you’ll get 6 ÷ 2(1 + 3) = 6 ÷ ((2 × 1) + (2 × 3)) = 6 ÷ (2 + 6) = 6 ÷ 8 = 3/4. This happens because the expression can be interpreted in different ways, resulting in different answers.
- 3(4 + 1) + 62 ÷ 3 — 7 = 3 × 5 + 62 ÷ 3 — 7 = 3 × 5 + 36 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20
It’s easy to make various mistakes in this expression, but the correct order is as follows: the first operation should be performed in brackets, then 6 should be raised to the second power, then you need to perform multiplication, then division, after which you do addition and subtraction. A similar result is obtained if you use the distributive property (where a(b + c) equals a × b + a × c) and solve the problem as follows: 3(4 + 1) + 62 ÷ 3 — 7 = ((3 × 4) + (3 × 1)) + 62 ÷ 3 — 7 = (12 + 3) + 62 ÷ 3 — 7 =
15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20.