Why We Can’t Divide by Zero

We were taught in school that we can’t divide by zero. There are even jokes that black holes appeared because some people tried to do it. But what happens if we do?

We, at 5-Minute Crafts, studied this question carefully and finally figured out what happens if we break this taboo.

What division is

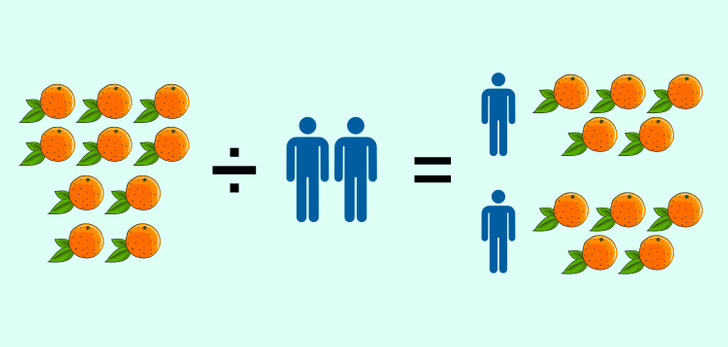
At a simple arithmetic level, division involves dividing a group of objects into equal parts. For example, let’s take 10 oranges that need to be divided between 5 people at a table. Each person will get the amount of fruit equal to 10 ÷ 5, or 2 each. If there was only one person at the table, they would get 10 ÷ 1, or 10 oranges.

So here is the question: How many out of 10 oranges will each person get if there are 0 people at the table?

Why we can’t divide by 0

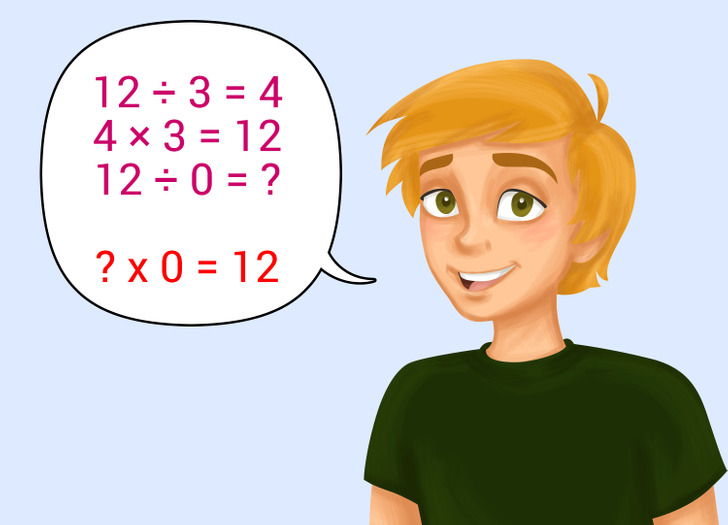
The thing is, division by 0 makes no sense because any attempt to do it leads to more and more controversy. Let’s look at this example.

As a rule, after division, we can get back by using multiplication. For the equation r = a ÷ b, a = r × b should be correct.
If we suggest that b = 0, we will get r × 0 = a.

If 12 ÷ 3 = 4, then 4 × 3 = 12.
If 12 ÷ 0 = ?, we are supposed to get ? × 0 = 12.

But since any other number multiplied by 0 equals 0, we would get r × 0 = 0.
So whatever with number stands behind r if a ≠ 0, the equation can’t be solved.

How about infinity?

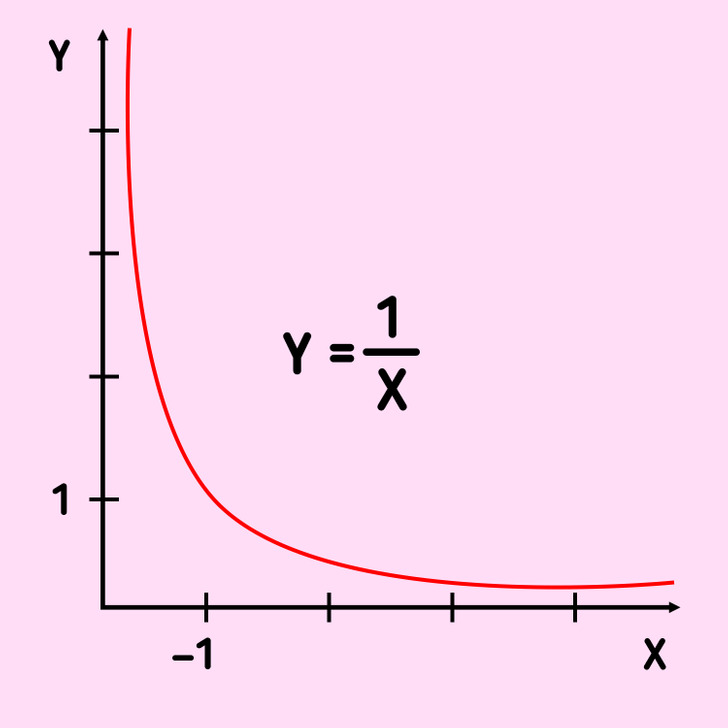
We can assume that a fraction whose denominator is 0 is equal to infinity. This idea does have logic. Perhaps you have noticed that when dividing numbers by smaller and smaller numbers, we get a bigger and bigger number. Here is an example:

20 ÷ 5 = 4

20 ÷ 2 = 10

20 ÷ 0,5 = 40

20 ÷ 0,0000005 = 40 000 000

It can be seen that the divisor decreases infinitely, and the quotient grows infinitely, thereby tending toward infinity. However, tending toward infinity and being equal to infinity are 2 completely different concepts. All because infinity is not a rigid number but rather an abstract idea. If we tried to treat infinity as a number (for example, in the equation 1 : 0 = ∞), then we would encounter the following mathematical anomalies:

1 ÷ 0 = ∞ = 2 ÷ 0
1 = 0 × ∞ = 2
Therefore,
1 = 2

In this scenario, we would get the statement that all integers are equal to each other, and the whole system would collapse.

What if we divide 0 by 0?

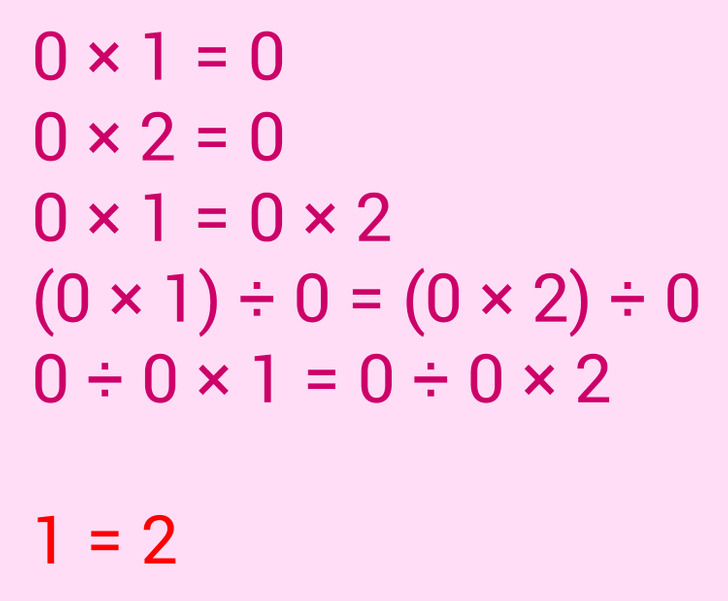
Let’s look at one more example:

Let’s suppose that
0 × 1 = 0
0 × 2 = 0
Then the following would be correct:
0 × 1 = 0 × 2
Dividing both parts by 0 gives:
(0 × 1) ÷ 0 = (0 × 2) ÷ 0
0 ÷ 0 × 1 = 0 ÷ 0 × 2
Or, to put it in more simple terms,
1 = 2

The mistake here is in the assumption that the same rules apply when dividing 0 by 0 as when dividing it by other numbers.

If we summarize everything said above, the rule, “It’s forbidden to divide by 0” becomes clearer: we can’t divide by 0 not because something critical will happen but because there is simply no sense in doing it.