How to Calculate Speed
We learned how to calculate speed in math class back in school. Then we’d use this knowledge during physics and other classes. But what should you do if you finished school a long time ago and this knowledge has somehow been erased from your memory?
5-Minute Crafts would like to tell you some basic facts about speed and how to calculate it.
What speed is
Speed tells us how fast an object is moving. This is a general term, and the concept of “speed” can be described in more detail by taking into account different types of speeds.
- Imagine that you are driving on a long road and need to cover a certain distance. Since it can be difficult to maintain the same speed all the time, you will move a little slower in some areas and a little faster in others. The ratio of the distance that you’ve covered to the time spent will be your average speed.
The average speed is the total distance traveled in a unit of time, like an hour.
- The speed at which an object is moving at a given moment or for a very short period of time is called instantaneous. You can find the instantaneous speed of a car by just looking at its speedometer.
The instantaneous speed is a change in the position of an object between 2 points in time, the time interval between which approaches zero.
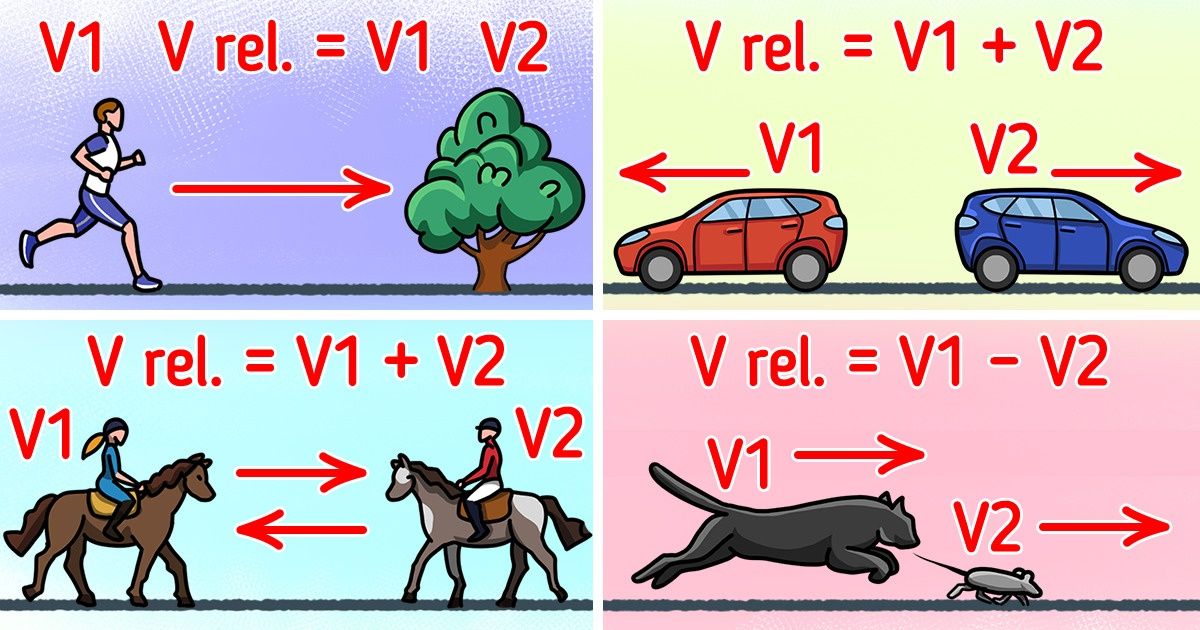
- If 2 objects are involved, then the speed of one in relation to the other will be referred to as relative.
The relative speed is the speed of one object measured in relation to another object.
There are 2 cases of relative speed. One of them considers objects moving in one direction, and the other considers those moving in opposite directions.
Example: 2 cars are driving on a highway. The speed of one in relation to the other will be considered relative, regardless of the direction in which the cars are moving.
- The average and instantaneous speeds relate to linear speeds. They reflect the distance traveled per unit of time. But when it comes to moving along a circular path, it would be correct to talk about the tangential speed.
The tangential speed is the linear speed of an object moving along a circular path.
- The concept of tangential speed is closely related to the concept of rotational speed, which reflects the number of revolutions made by an object within a certain period of time.
The rotational speed is the number of complete revolutions that an object makes per unit of time.
How to calculate the average speed
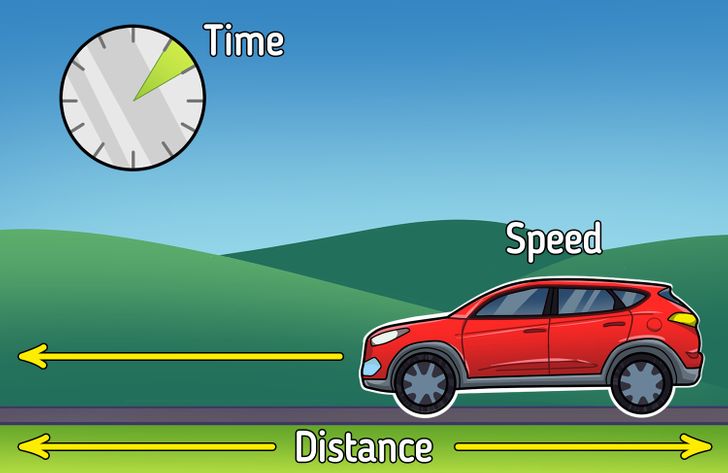
In order to calculate the average speed of an object, you need to know the distance covered by this object and the total elapsed time of its whole journey.
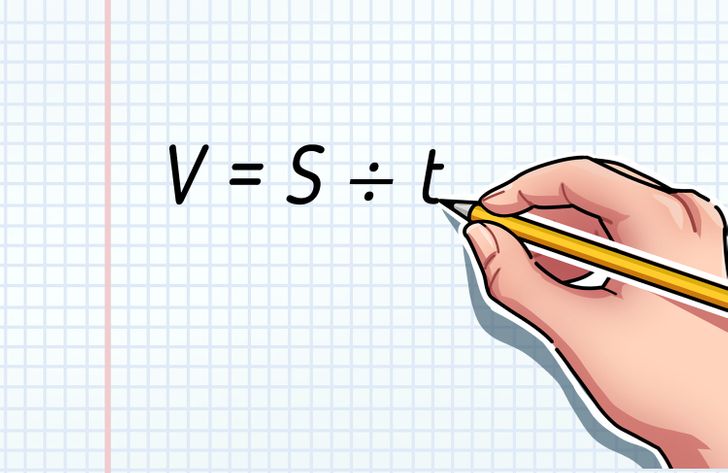
The formula for speed is V = S ÷ t where “V” is speed, “S” is distance, and “t” is time spent.
Let’s consider an example: The car was moving along the highway for 2 hours and during this time traveled a distance of 160 miles. By applying the formula V = S ÷ t, you can find the speed of the car: 160 (mi) ÷ 2 (h) = 80 (mph).
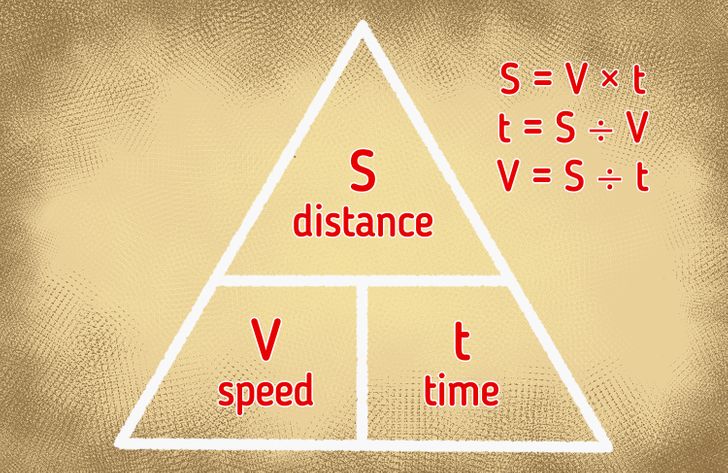
To easily remember the formula, use the distance-speed-time triangle. With its help, you can calculate not only the speed but other values as well.
- Distance = speed × time (S = V × t)
- Time = distance ÷ speed (t = S ÷ V)
How to calculate the relative speed
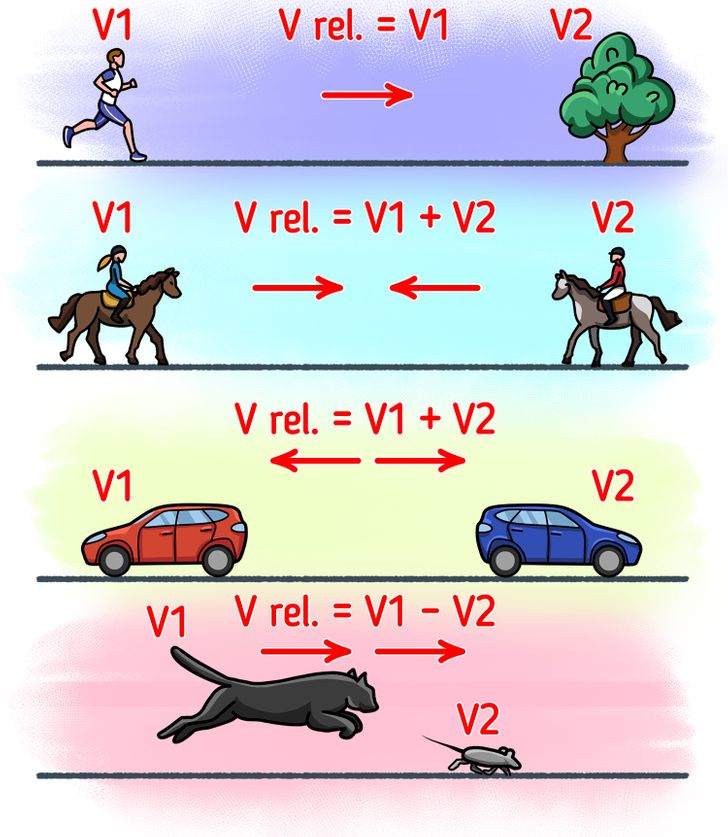
- The relative speed for 1 moving object and 1 stationary object will be equal to the speed of the moving object since the speed of the stationary object is 0. So, V rel. = V1.
- If 2 objects are moving in opposite directions at different speeds, the relative speed will be equal to the sum of the 2 speeds: V rel. = V1 + V2 where V1 is the speed of the first object, and V2 is the speed of the second object. You can also find the time by the formula t = S ÷ (V1 + V2), and the distance — S = (V1 + V2) × t.
❗ Please note that in this case, 2 objects can either move toward each other or move from one point away from each other. - If 2 objects are moving in the same direction at different speeds, the relative speed will be calculated using the formula V1 — V2, where V1 is the speed of the first object, V2 is the speed of the second object, and V1 > V2. V rel. = V1 — V2. Based on the above, the time after which the objects will meet can be calculated by the formula t = S ÷ (V1 — V2), and the distance S = (V1 — V2) × t.