2 Nerdy Tricks to Find a Cube Root in Seconds

Math may not be everyone’s favorite, but knowing the tricks to quickly solve complex and challenging questions is super fun, plus, it improves your intelligence and IQ. Imagine finding yourself in a situation where you had to calculate the cube root of 636,056. Think about how you’d solve that in 3-5 seconds without a calculator. Be proud of yourself if you’ve found the answer, which is 86.
If you couldn’t solve that one, 5-Minute Crafts is ready to share some secret tips and tricks with you. Read on to learn more.
Finding the cube root
- Let’s learn the very basics first. In math, if a natural number is multiplied by itself (twice), we say that the number is squared. When multiplied by 3 times or raised to power 3, it’s cubed. If n is the natural number, the cube of it is n3.
- When the same number is multiplied thrice, and if the result is the same number’s cube, we call that natural number a ’’perfect cube,’’ like, for example, 1, 8 (23), 27 (33), 64 (43), etc.
- The cube root is the reverse process of finding the cubed number and is denoted as ∛. For example, when 5 is cubed, we get 125. When we take the cube root of 125, we get 5.
Way 1: Use the estimation method for large numbers.
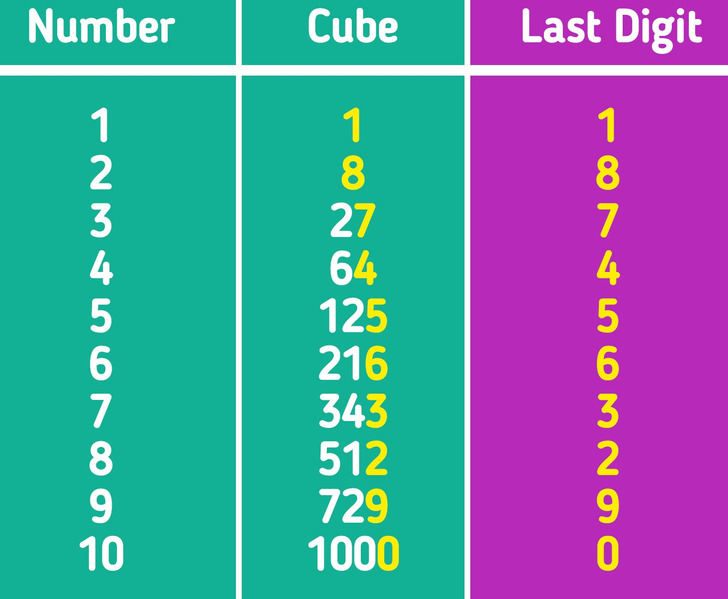
- To do the trick, first memorize or write down the cube of numbers 1 through 10. The cube of 1 is still 1, the cube of 2 is 8, the cube of 3 is 27, and so on. You’ll see the pattern repeated for 11-20 and 21-30; the last digits (unit digits) stay the same.
- Only focus on the last digits of the cubed numbers. An easy way to remember it is for the numbers 1, 4, 5, 6, 9, and 0, the last digit is the same as the numbers; but it flips for the numbers 2 and 8 and 3 and 7.
- The cube roots of 4, 5, and 6 digit-long numbers will always be 2 digits long.
Example 1: Find the cube root of 39,304.

- First, we’ll work on the last 3 digits. Look at 39,304; the very last digit is 4. Looking at our table, it corresponds to the cubed 4. So, write down the number 4.
- Ignore the last 3 digits, 304.
- Let’s find 39’s cube root, which stays between 27 and 64. Take the closest one to 27; it’s most comparable to the cube of 3.
- We’ve found the other part of our answer, which is 3.
- Finally, when you put the numbers together, the answer is 34.
Example 2:
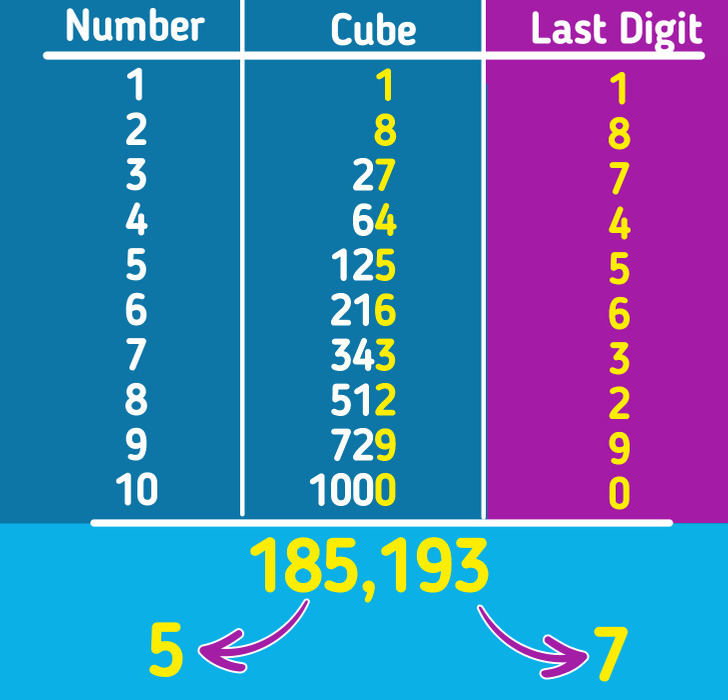
Look at the last digit of 185,193. It’s 3, and based on our table, it corresponds to the number 7. Ignore the last 3 digits; now we have 185, whose cube root is close to 5. Put 5 and 7 together, and the answer is 57.
Way 2: Use the prime factorization method.

- All you need to do is factorize the number and find the prime numbers of it. Let’s work on 216.
- When factorizing 216, we get 2 × 2 × 2 × 3 × 3 × 3. As you see, we have three 2s and three 3s. You can take one number from each group and write it as 23 × 33 = 63. Then we get the cube root of 216, denoting 3√216 = 6.
- Here, we also see that 216 is a perfect cube.
Bonus 1: how to make a perfect cube
Imagine an egg rack with 6 shelves and a 6×6 egg capacity. If there are 108 eggs, to make it a perfect cube, all you need to do is the following.
- Find the cube root of 108 by prime factorization: 108 = 2 × 2 × 3 × 3 × 3.
- As you can see, the result isn’t a perfect cube. To be able to call it a ’’perfect cube,’’ it must be grouped in triples.
- There are three 3s but only two 2s. Therefore, we need to add one more 2, which means we must multiply both sides by 2. After that, we get: 108 × 2 = 2 × 2 × 2 × 3 × 3 × 3 = 216.
- As a result, we need 108 more eggs to make it a perfect cube.
Bonus 2: interesting cube patterns

- If you list the odd numbers and take the sum of them in ascending order starting from 1, then take their cubes, you get an exciting pattern of n3.
- Start with the odd natural number, 1, then write down its cube value, which is also 1.
- Then add the following 2 consecutive odd numbers, 3+5, which is 8, and it can be written as 23.
- Get the sum of the following 3 consecutive odd numbers, 7+ 9 + 11 = 33, and so on.
- So, if you want to find the sum of n odd natural numbers, you get n3.
