How to Add and Subtract Fractions
A fraction is a way of mathematically expressing a divided quantity. It is composed of the numerator, which indicates how many parts we have; and the denominator, which are the parts into which the unit is divided.
5-Minute Crafts is showing you how to solve this type of operation, whether or not the fractions contain common or different denominators.
The parts of a fraction

- Numerator: the number of parts you have
- Denominator: the total number of parts
Types of fractions

- Proper fraction: The numerator is less than the denominator.
- Improper fraction: The numerator is greater than the denominator.
- Mixed fraction (or mixed number): They have a whole part and a proper fraction.
Fractions with a common denominator
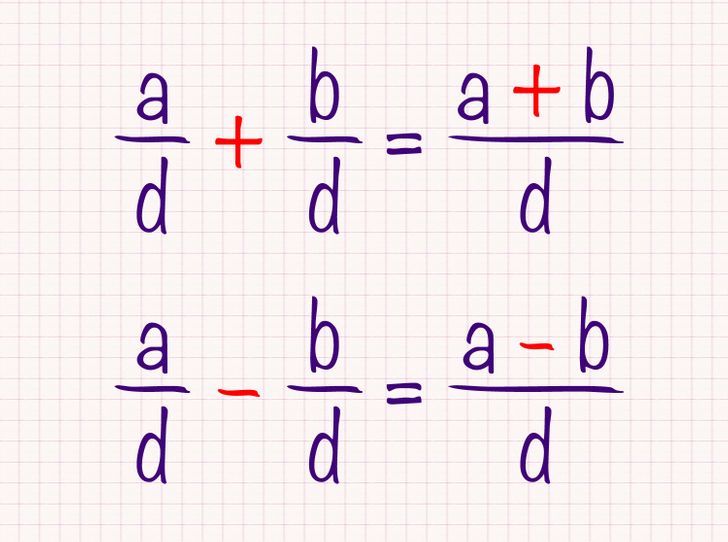
To solve fractions with a common denominator, add or subtract the numerators as usual, and keep the same denominator.
Addition and subtraction of fractions with common denominators
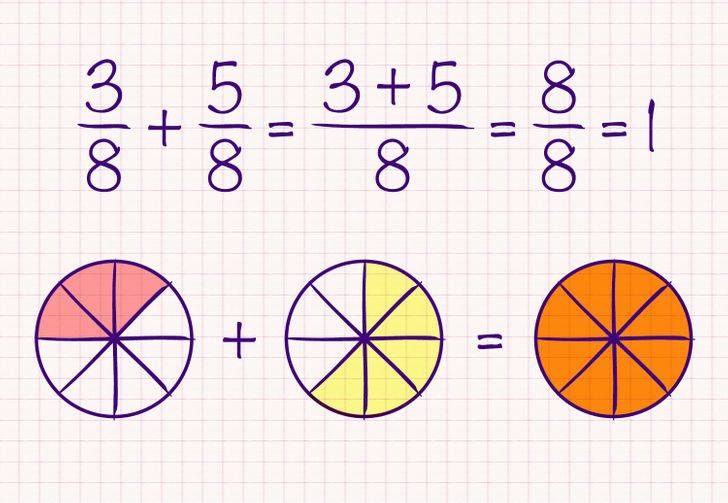
Let’s consider the fractions 3/8 and 5/8 as an example.
- Add the numerators 3 + 5 and leave the same denominator of 8. The answer would be 8/8, which, when simplified, will give us the number 1 as a result.
Now, for subtraction, we’ll use the fractions 5/7 and 3/7.
- To subtract fractions with the same denominator, the same procedure is used. Just subtract the numerators (3 from 5) and leave the same denominator, and you will obtain 2/7 as a result.
Fractions with a different denominator
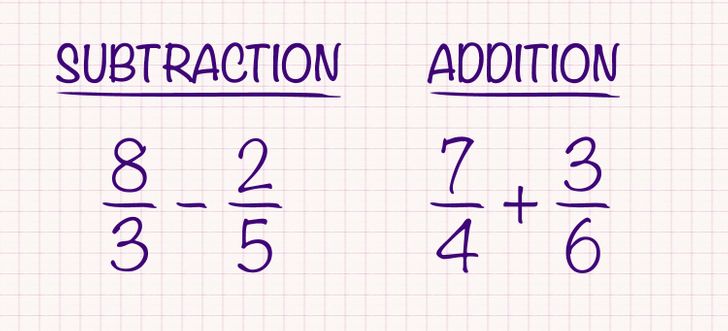
When fractions don’t have the same denominator, there are 2 methods that can help you solve them. The first one is called the lowest common multiple (or least common multiple), and the second one is called cross-multiplication.
Least common multiple

The first method we will explain to solve this type of operation is called the least common multiple (or lowest common multiple), which is the least common multiple that we can find between the denominators.
As an example, we’ll take the denominators 4 and 6. Multiply each of these numbers by all the numbers starting from 1 (then 2, 3, and so on) and stopping only until you get a multiplication result that is common to both (this result is the lowest common multiple). For this case, the least common multiple is the number 12. We can also see that the number 24 is common for both denominators, but that number is not the lowest one that they both have in common.
The sum of fractions with the lowest common multiple

For example, we will add the following fractions: 9/12 + 5/8.
- Find the smallest common number you get by using the multiplication tables of both numbers in the denominators 12 and 8. In this case, the number we get is 24.
- Then divide 24 by the first denominator and multiply it by the first numerator.
- Now repeat this step for the second fraction. The sum of these 2 new numbers, which are now on top of a single common denominator (24), obtained by the lowest common multiple method, will give us a new numerator for our new resulting fraction.
Note: You can simplify this fraction if there is a number that divides both the numerator and the denominator. Sometimes this can give us a whole number as a result.
The addition of fractions with cross-multiplication
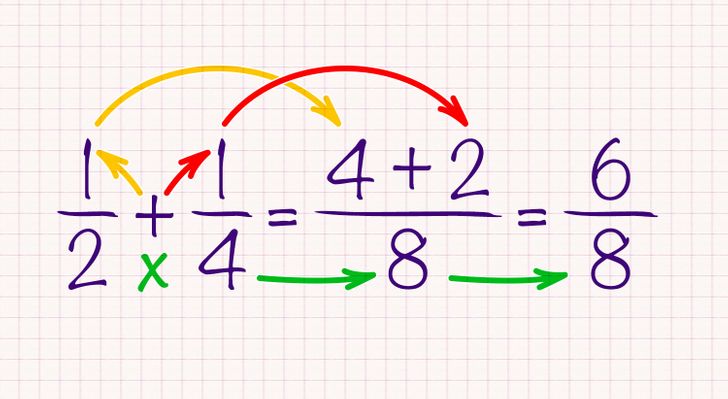
Let’s take, as an example, 1/2 + 1/4.
- Multiply one denominator by the other (denominator) and use this result as the common denominator. In this case, the result will be 8.
- Then multiply the second denominator by the first numerator and place it as the first number on top of the common denominator of the new fraction after the equal sign.
- The second number on top of the common denominator in the new fraction is obtained by multiplying the first denominator by the second numerator.
- The resulting fraction is the sum of these results with the denominator obtained from the first multiplication.