How to Calculate a Square Root by Hand
The square root of any given number x is a number y such that y2 = x. In other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. Although it may seem a complex and somewhat tedious operation, it’s actually very easy to calculate by hand, you just have to know the steps to do it.
5-Minute Crafts is explaining the procedure, step by step, to help you to become a math whiz.
Parts of a square root
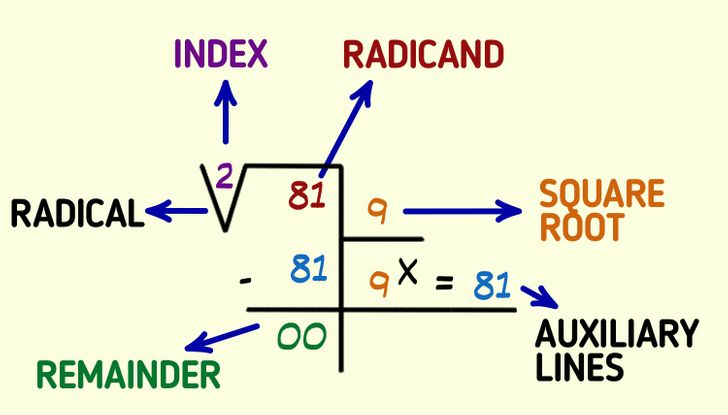
- Radical: This is just the symbol that indicates if the calculation you will have to perform is a square root.
- Index: Typically, when you have to solve a square root, the index equals 2. That’s because it’s a convention, and you typically don’t have to write 2 anywhere unless you’re actually using a different index (like 3 or 4). That means you can leave an empty space instead of just writing a 2.
- Radicand: This is the number from which the square root needs to be obtained.
- Square root: It’s the place where you’ll write the result of your operation.
- Auxiliary lines: These are the spaces where you’ll solve the mathematical operation, leading to the final result of the square root.
- Remainder: This is the sum you’re left with when the calculation is finished.
Types of square roots
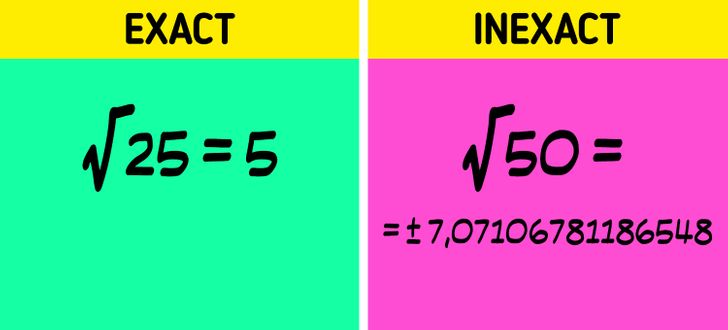
- Exact: This type of square root can only be obtained with numbers that are a perfect square of each other, i.e., numbers whose square root is a natural number. At the end of the calculation, the remainder will be equal to 0.
- Inexact: This is pretty much all the other numbers that are not an exact square number. Because of this, the square root of these numbers cannot be solved without resorting to decimal numbers, and when performing the corresponding divisions, the mathematical operation will result in a remainder.
Calculating a square root

To explain the process, we will take the natural number, 50,419, as an example, and we’ll try to find its square root.
1. Split the digits of the radicand from right to left in pairs. In this particular example, you’ve probably noticed that our number has 5 digits, so the last group of digits will be one digit longer than the rest.
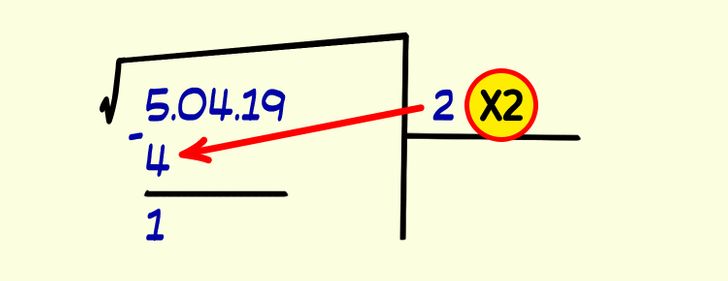
2. Find a number that when multiplied by itself comes as close as possible to the first digit of the radicand. Place that number in the square root space. Then subtract the multiplied number from the first digit of the radicand and write down the result.
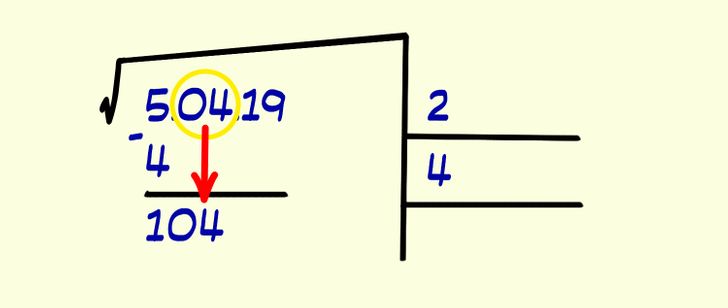
3. Lower the next 2 digits of the radicand (digit 2 and 3 from left to right) by writing them next to the remainder of the subtraction. Just like you wrote the first number you found (the 2) in the square root row before, write its double (4) in a row just below it.
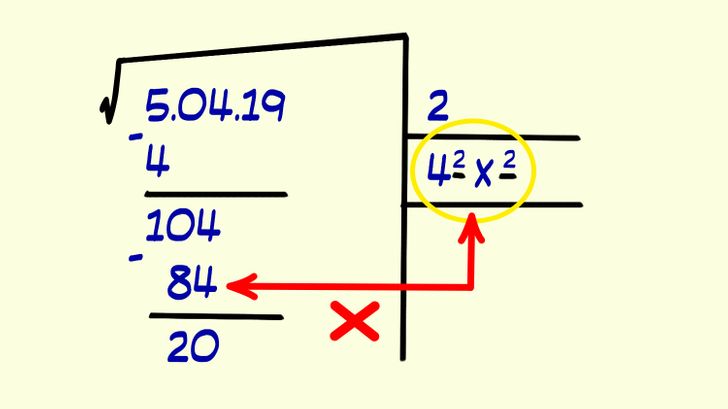
4. Find a number between 0 and 9 and place it to the right of the 4 in the auxiliary lines. Then multiply 42 by the number you chose (in this case 2), but you always have to make sure that the result (84) does not exceed the number located in the remainder area (104); if it does, you must choose a smaller number. Subtract these 2 numbers and write down the result.
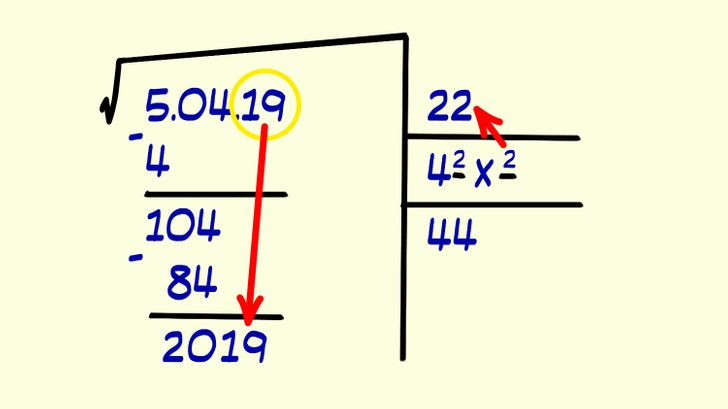
5. Lower the remaining digits of the radicand. Write the number you found (the 2) in the square root space (it will now be 22). Just like you did before, write the double number (44) in the auxiliary lines.
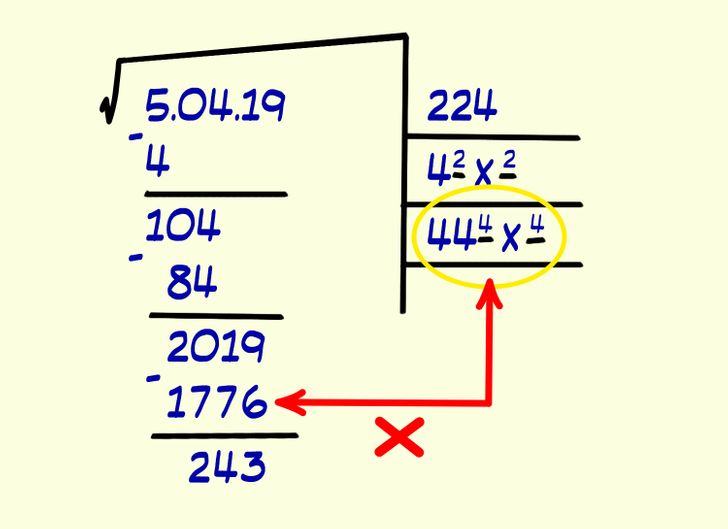
6. Once again, find a number between 0 and 9 and place it to the right of 44. In our example, you’ll be left with the number 444. Now multiply 444 by 4 (the number you chose). Make sure that the result does not exceed the number in the radicand (2019). Subtract them. Write the number you found (the 4) in the square root area.
Obtaining the decimals
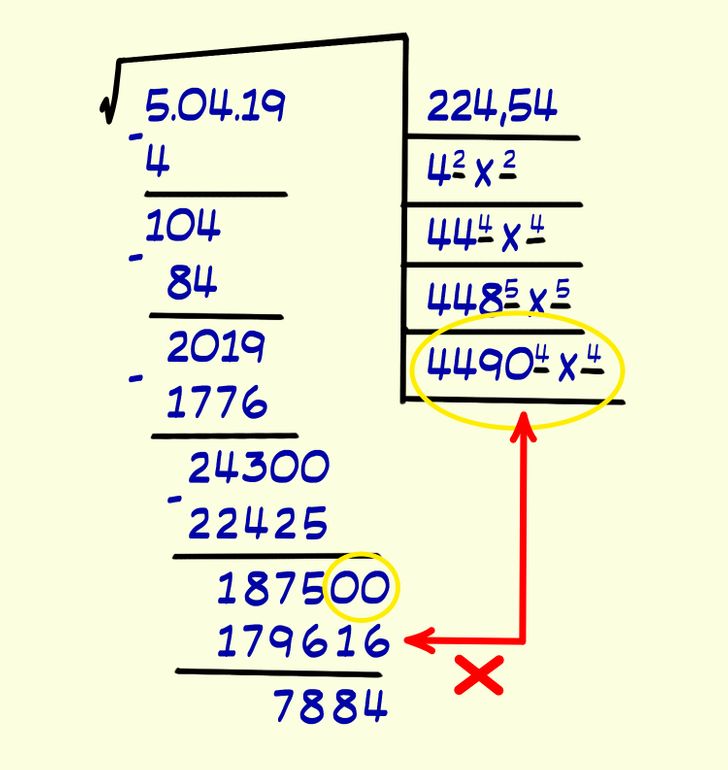
- If there are no more numbers left to move down in the radicand and you want to continue with the operation and get decimals, add 2 zeros and start doing the procedure as you have been doing it. That is to say, you should start by lowering twice the number that’s in the square root area, then look for a figure between 0 and 9, which you will add to the right of the number you lowered.
- Repeat the procedure to obtain more decimals.