How to Solve Quadratic Equations
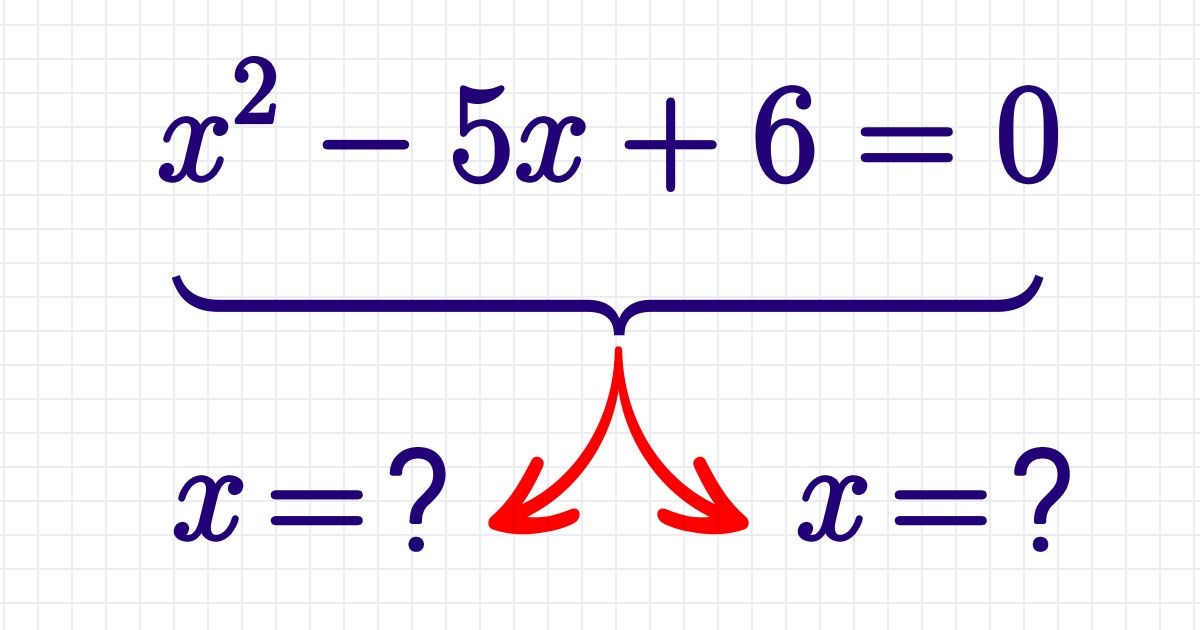
Solving quadratic equations is an important topic in school. If you want to brush up on your knowledge, help your teenage children, or learn something new, use our simple instructions.
We at 5-Minute Crafts decided to make the task as simple as possible for those that have trouble with quadratic equations.
What a quadratic equation is
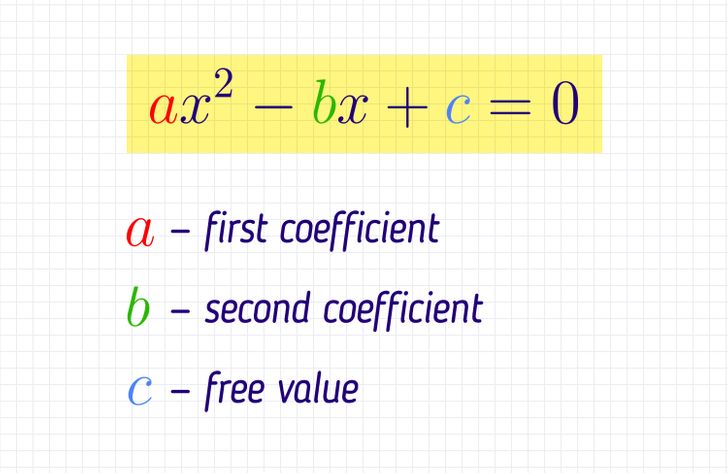
It’s an equation like this: ax2 + bx + c = 0.
- a — first coefficient
- b — second coefficient
- c — free value
Practice looking for a, b, and c.
Examples:
- x2 + 5x = 0. Here, а = 1, b = 5, and c = 0.
- 3×2 + 8x — 7 = 0. Here, а = 3, b = 8, and c = —7.
- —x2 — 3x + 15 = 0. Here, а = —1, b = —3, and c = 15.
- 5×2 = 0. Here, а = 5, b = 0, and c = 0.
- x2 — 5 = 0. Here, а = 1, b = 0, and c = —5.
How to solve a quadratic equation, step № 1
The equation has to look like this: ax2 + bx + c = 0. The right side should be 0.
Examples:
- x2 — 3x — 5 = 11 — 3x
x2 — 3x — 5 — 11 + 3x = 0
x2 — 5 — 11 = 0
x2 — 16 = 0
We made the equation look like this: ax2 + bx + c = 0, where а = 1, b = 0, and c = —16.
How to solve a quadratic equation, step № 2
A universal method to solve quadratic equations is using this formula:
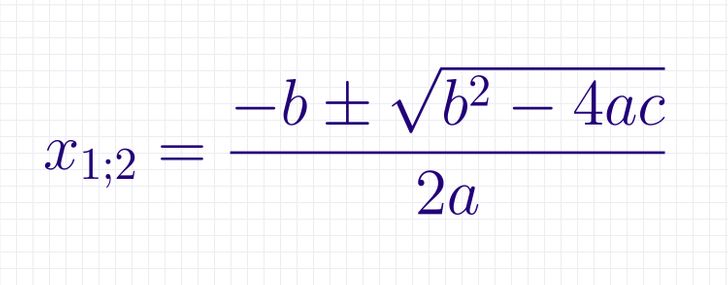
Using this formula, you can solve any quadratic equation.
b2 − 4ac is often replaced with D. D is discriminant.
How to solve a quadratic equation using the formula
Check how to solve a quadratic equation.
- Write down the quadratic equation.
- Write down the formula.
- Find the coefficients. а = 1, b = —5, and c = 6.
- Replace a, b, and c in the formula with 1, —5, and 6.
- Do the calculations.
- As the discriminant is positive, the equation has 2 roots.
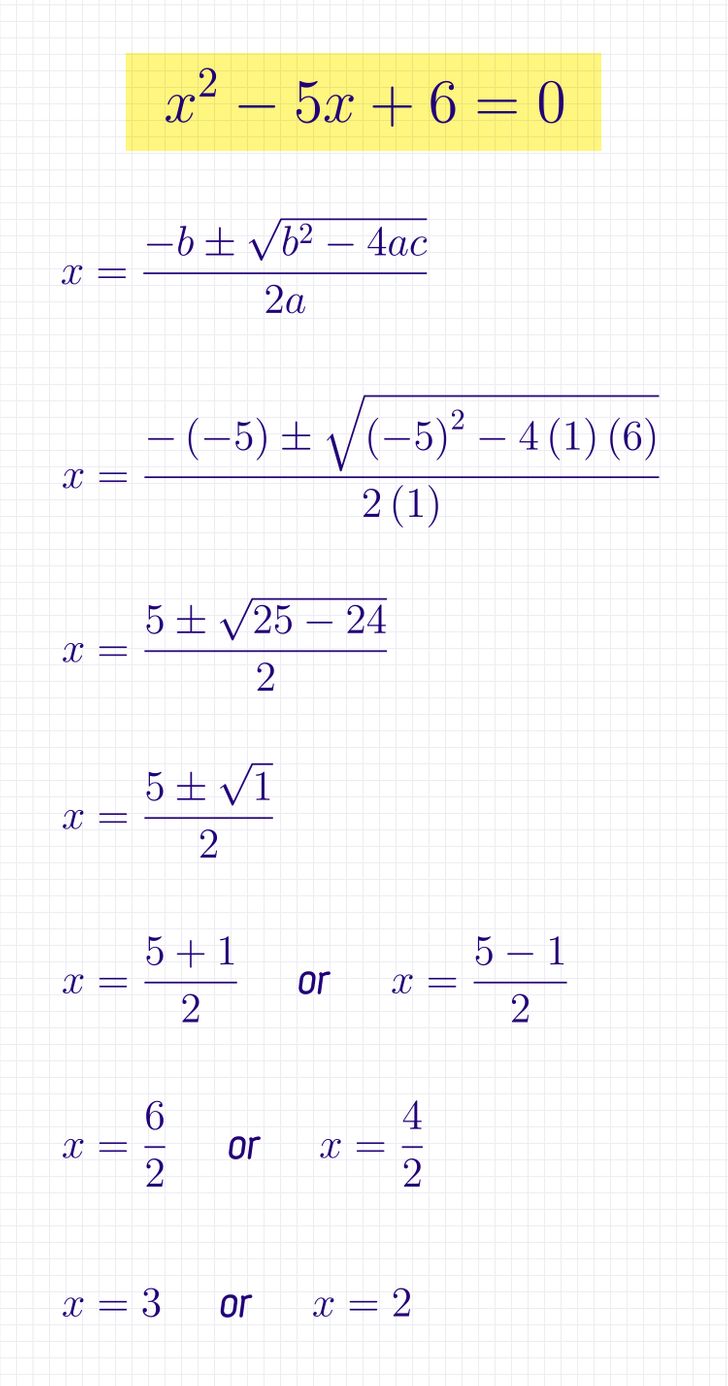
What the discriminant tells us
If the discriminant is more than 0, the equation has 2 roots.
If the discriminant is 0, the equation has 1 root.
What if the discriminant is less than 0? There’s a rule: you can’t take a square root from a negative number. If the discriminant is less than 0, there are no real roots.