Negative Numbers and How to Solve Equations With Them

When we count something, we use natural numbers. For example, first, we cut 1 piece of a cake, then we cut another one and we have 2 small pieces of cake. Or we collect apples, we take 1, then another 1, and we have 2 apples. We add numbers to each other using addition. If we use subtraction the same way, at a certain point, we will have to deal with negative numbers.

5-Minute Crafts explains what negative numbers are, what’s special about them, and what we should know when using them.

What a negative number is

It might seem like negative numbers are not really necessary. But if you walk into an elevator in a mall, you will see floors of the parking lot that are usually underground and they are “-1” and “-2.”

There are negative numbers on our thermometers: when it’s cold outside, the temperature is below 0° Celsius.

So, negative numbers are those that come before 0. Let’s draw a number line.

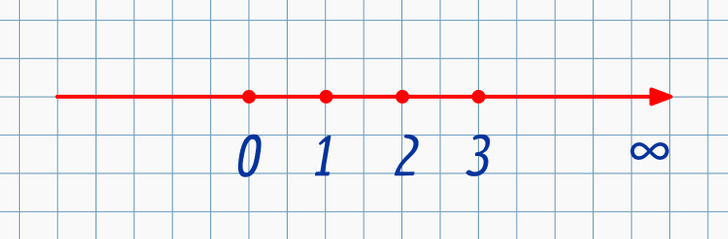
Draw a line on graph paper. Mark the starting point of 0. Now, go 2 squares right and make another mark. This is 1. You can do the same for as long as you want. These numbers are bigger than 0, so they are positive numbers. Sometimes, we add a + next to them, so +1 = 1, and 1 = +1.

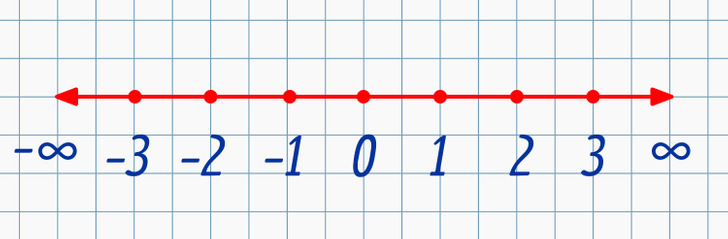
If we go left, we will see numbers that are less than 0. This is why they are called negative numbers and we use a — before them. And −1 is not the same as 1. Negative numbers are symmetrical compared to positive numbers and 0 is neither.

If 0 is nothing, how can something be less than nothing? 0 is also a starting point that separates the numbers on the line. Let’s imagine you had $100 in your bank account. After going to the store, you have -$100. How much money do you need to add to the balance to make it $100 again? If you add just $100, the negative number will go away and the balance will be 0. If you add another $100, the balance will be positive again and be $100.

This is clear if you look at the line. For each natural number, there is only 1 negative number. If you add 100 to −100, you will have 0. If you add −100 to 100, the result will be the same. So, the conclusion is this:

• (-a) + (+a) = 0
• (-a) + 0 = (-a)
• -(-a) = a

How to compare negative numbers

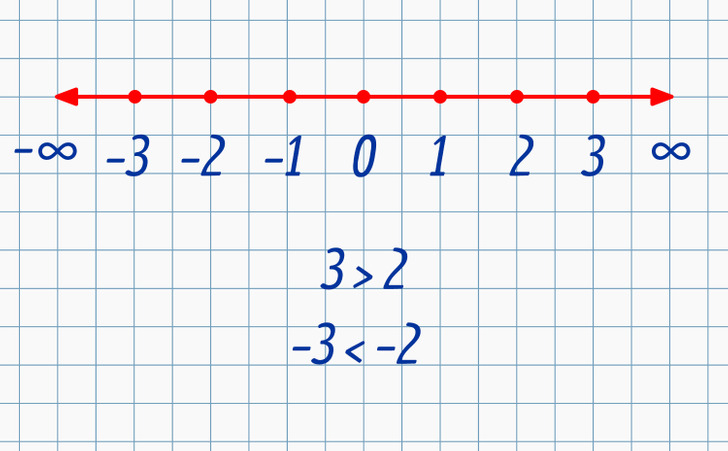
All negative numbers, just like the positive ones, are on the line in a certain order. It allows us to compare them. But there are certain features: if one positive number is bigger than another, it’s further to the right. In other words, number 3 is bigger than 2 because it’s further to the right. With negative numbers, it’s different: −3 is less than −2 because it’s further to the left.

Operations with negative numbers

The symbol before the number has to be taken into account because it determines the result.

• When adding 2 positive numbers, we always get a positive number: 2 + 3 = 5.
• When adding 2 negative numbers, we always get a negative number: (-2) + (-3) = (-5). To see why this happens, look at the number line: if you add −3 to −2, we go even further to the left.

• When adding a positive number to a negative one, if the positive one has a bigger absolute value, the result is a positive number: 5 + (-3) = 2. We are basically subtracting 3 from 5, so the result is 2.
• When adding a positive number to a negative one, if the negative one has a bigger absolute value, the result is a negative number: 5 + (-10) = (-5). You’re adding 5 to −10, so the result is −5.

Advice: It might be easier if you remember the rules of bracket removal. For example: (+5) + (-3) = 5 − 3 = 2. Or (+5) + (-10) = 5 − 10 = (-5).

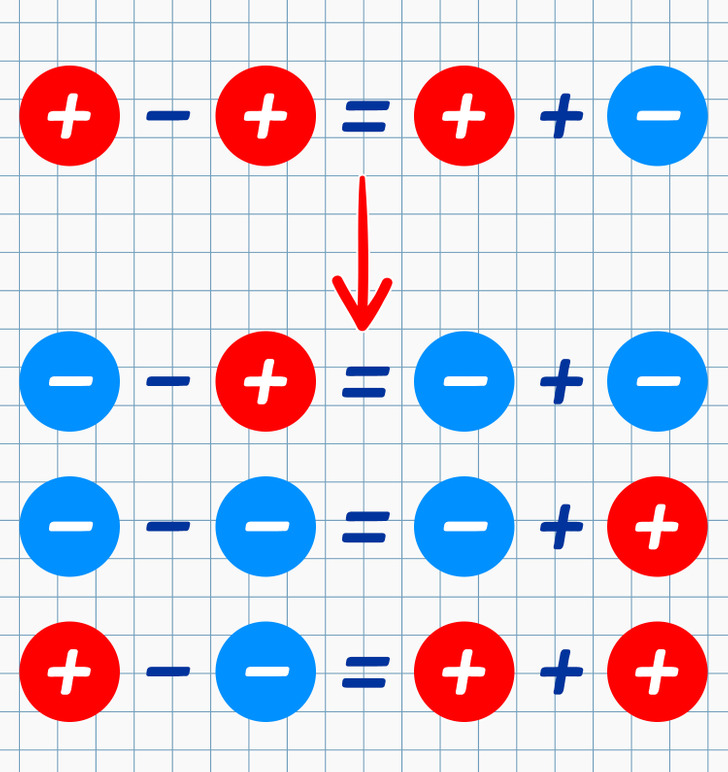
• Because subtraction is an opposite operation, you need to add the number opposite to the one you’re subtracting: (-2) − (+5) = (-2) + (-5) = (-7). Or 5 − (-2) = 5 + (+2) = 7.

When can you use it in real life? Imagine the temperature was −2°C and now it’s 10°C less. What’s the actual temperature now? You need to subtract 10 from −2 or add −10 to −2. So, it’s −12 °C.

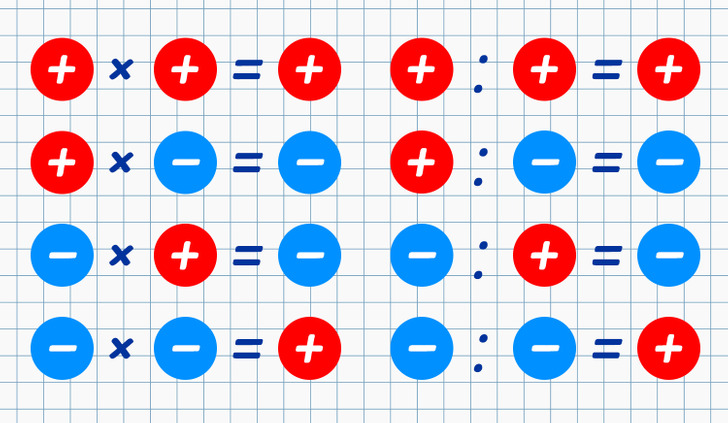
• When multiplying and dividing numbers, follow the rule of signs: the result of dividing or multiplying numbers with different signs is negative, and the same signs — positive. (-а) × (-b) = a × b.

Let’s say a husband and a wife have debts. Each of them is $100 in debt. What’s the debt in total? You need to add both debts: (-100) + (-100). Or you can multiply 1 debt by 2: (-100) × 2. As a result, you get -$200.

• If you need to put a number into a negative power, reverse the expression by writing it down as a fraction with 1 in the numerator and the starting number in the denominator. Replace the number of the power with a positive number and do this: a⁻ⁿ = 1/aⁿ.