How to Do Math Problems With Parentheses

There’s a lot of confusion in the order of actions in math problems. The situation gets even more complicated when there are parentheses that change the order of operations.

5-Minute Crafts has collected all the things you should keep in mind when you are doing a math problem with parentheses.

The order of operations in problems without parentheses

To solve simple problems without parentheses, find all the roots, and solve fractions, remember these rules:

• All the actions are done left to right.
• First, do multiplication and division, and then addition and subtraction.

How to use these rules?

Example № 1. Calculate: 15 − 3 + 7.

First, do all the actions left to right:

1) 15 − 3 = 12

2) 12 + 7 = 19

The answer: 15 − 3 + 7 = 19.

Example № 2. Calculate: 10 ÷ 2 × 8.

Also do the actions from left to right:

1) 10 ÷ 2 = 5

2) 5 × 8 = 40

The answer: 10 ÷ 2 × 8 = 40.

Examples № 3. Calculate: 5 × 4 − 8 ÷ 2.

Also go left to right but keep in mind that multiplication and division are done first. So:

1) 5 × 4 = 20. This is multiplication and it’s first if you go left to right.

2) 8 ÷ 2 = 4. This is division and even though it’s after the subtraction, you do the division first.

3) 20 − 4 = 16. Now, the usual order: after multiplication and division, go to subtraction.

The answer: 5 × 4 − 8 ÷ 2 = 16.

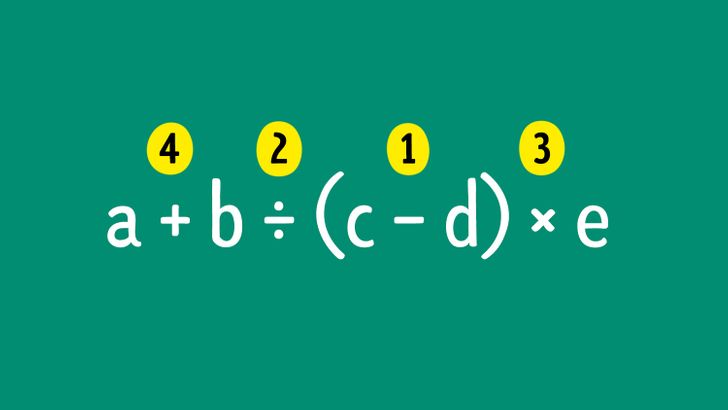
If there are several actions you have to do, you can number them at first until you memorize the right order.

Important: There’s no need to put the parentheses if addition and subtraction are done from left to right. For example, instead of (4 − 2) + 3, you can just write 4 − 2 + 3. Also, there’s no need for parentheses when it’s the actions that are prioritized anyway. For example, instead of 5 + (4 × 3), you can just write 5 + 4 × 3 because multiplication goes first anyway.

The order of operations in problems with parentheses

A problem can contain parentheses that are there to change the usual order of math actions. To do it right, remember the following rules:

• First, do all the actions in parentheses.
• Then, do the rest from left to right.
• Multiplication and division always go first, and then subtraction and addition.
• The same rules apply to the parentheses.
• If there are fractions or exponents, they should be calculated (if possible) before all other operations.

How to use these rules?

Example № 1. Calculate: 5 × (8 − 4) ÷ 2.

First, do the parentheses operations and then follow the regular order:

1) 8 − 4 = 4

When you know the result in parentheses, you can write down 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Then, follow the order:

2) 5 × 4 = 20

3) 20 ÷ 2 = 10

So, 5 × (8 − 4) ÷ 2 = 10.

The answer: 5 × (8 − 4) ÷ 2 = 10.

Example № 2. Calculate and compare the results: 7 − 3 + 2 and 7 − (3 + 2).

Calculate the result of the first expression: 7 − 3 + 2 = 6. Now, find the result of the second expression: 7 − (3 + 2) = 7 − 5 = 2. The parentheses in the second example changed the order of the operations, so the results are different.

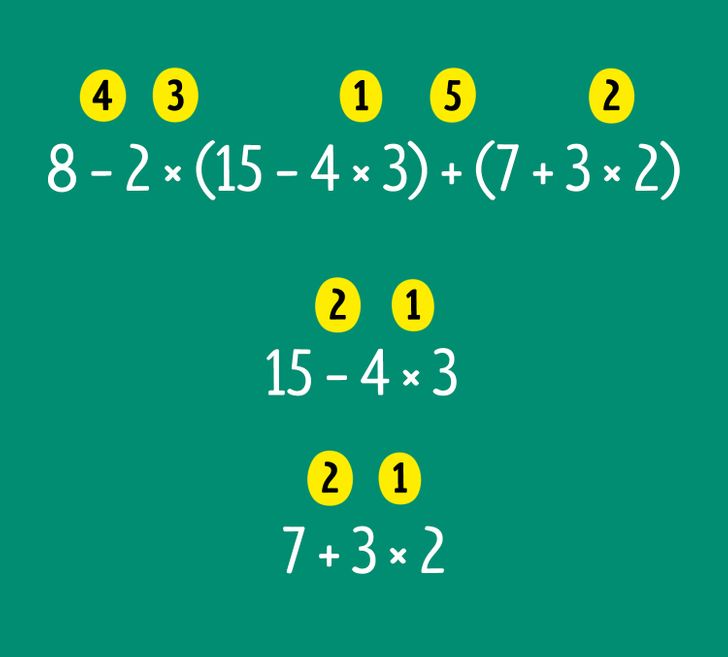
Example № 3. Calculate 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2).

At first, this expression seems complicated. To make the process simpler, split it into separate operations:

1) First, do the operations in parentheses. To get the right result in the first parentheses, remember the prioritized operations. So, calculate 4 × 3 and then subtract the result from 15. The answer is 3. Do the same with the second parentheses: calculate 3 × 2 and add 7. The answer is 13.

2) Now, write down 8 − 2 × 3 + 13. Now, do the multiplication and then subtraction and addition: 8 − 6 + 13 = 2 +13 = 15. The answer: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15.

Important: You can see expressions where there are parentheses inside other parentheses. It’s the same rule: first calculate everything in the inner parentheses, then the outer, and then do the rest. The type of parentheses may be different: most of the time, it’s ( ) but { } and [ ] can also be used.

Frequent mistakes with parentheses that lead to mistakes

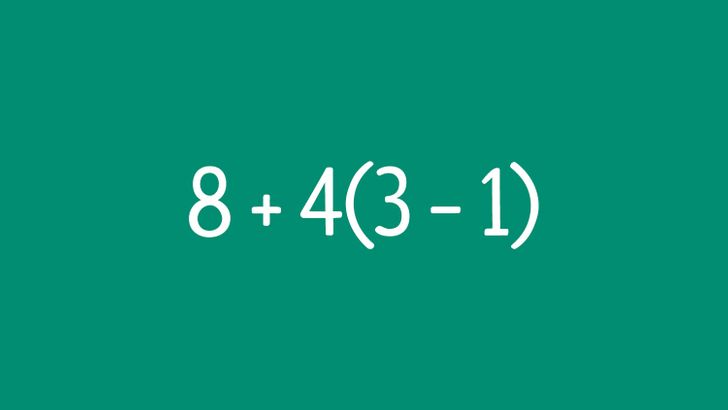
• The multiplication symbol is omitted before parentheses which might lead to confusion.

For example, you need to calculate 8 + 4(3 − 1). When solving this problem, it’s easy to confuse the order. The right order is this: first, calculate the result in parentheses, then multiply it by 4, and add the result to 8. So, you get this: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16.

This might seem a little more complicated: 8 ÷ 4(3 − 1). But the order is the same. First, do the parentheses and then do the division and multiplication from left to right: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.

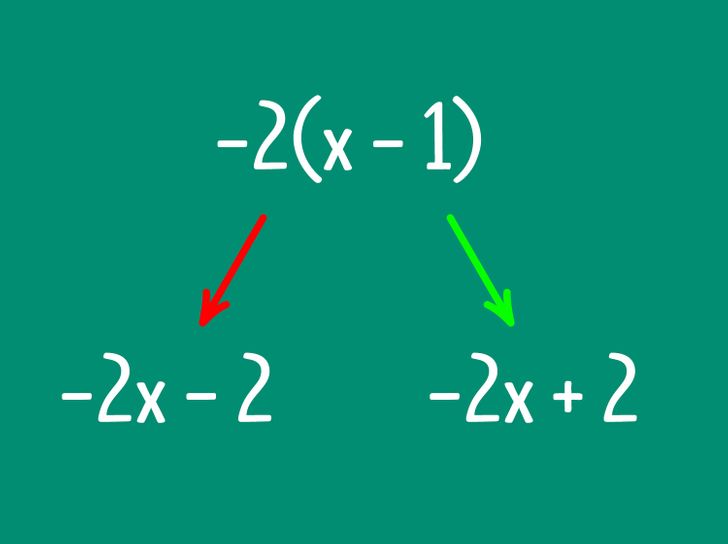
• Removing the parentheses with a minus before it incorrectly

There are situations when you need to remove parentheses to simplify the expression. In this case, if there is a minus before the parentheses, all the pluses and minuses should be replaced with their opposites. For example, 6 + 5 − (4 + 3 − 2) turns into 6 + 5 − 4 − 3 + 2. Very often, people make mistakes with variables and many operations, such as 3 + 2(x + 1) − 2(x − 1). Because we don’t know the variable, we can’t calculate the result in parentheses, so we need to remove the parentheses and turn it into 3 + 2х + 2 − 2х + 2 = 7. If you make a mistake, it will look like this: 3 + 2х + 2 − 2х — 2 = 3.

• The calculations are done on a calculator

Not all calculators can do the operations in the correct order even though there are some models that can tell simple operations from complicated ones. How can you check your calculator? Try calculating 1 + 5 × 7. If the answer is 36, your calculator can solve complicated problems.