How to Explain Fractions to a Child
Schoolchildren often experience difficulties while mastering the topic of fractions and operations with them. However, kids will understand fractions well from the start if you relate them to real life context and explain the basics through fun games and familiar concepts.
We at 5-Minute Crafts offer a simple guide that will even make it easy for a preschool-aged child to understand fractions and decimals.
What is a fraction?
There is a delicious pizza and 2 hungry people. Divide the whole pizza into 2 equal portions so that each gets a half. Half or 1/2 of a pizza — this is what we call a fraction. The 2 halves make up a whole.
You can draw 2 conclusions from the example above:
- a fraction is a part of a whole
- a fraction is less than an integer
Suppose, you had one pizza and divided it into 4 pieces. Someone ate one of the pieces, thus, you have 3 pieces out of four left. This can be expressed as 3/4. Note that on paper, the division bar may be horizontal or oblique.
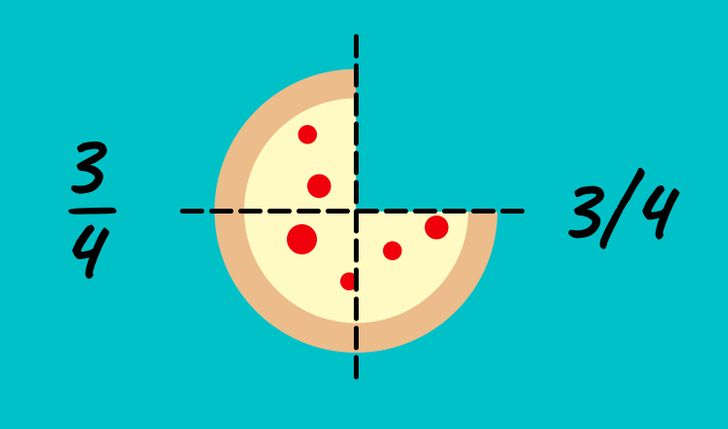
- The bottom number (or the right one) is the Denominator and shows how many equal parts the item is divided into.
- The top number (or the left one) in the fraction. It shows how many parts you have.
For example, there are 2 pizzas: you divided one equally between 2 people, and the other one — between 4. In the first case, each person received half of the pizza (1/2), and in the second one, only a quarter (1/4).
With these simple examples and tools, you can explain to your kids how to divide the whole into parts and what simple operations can be performed with fractions.
Method № 1: Using Legos

Lego pieces work well to show the different parts of the whole. The number of studs on each brick helps to better convey the concept of parts of the whole.
- If you take a piece with 8 studs as a whole, a square part with 4 studs will form half, with 6 — 3/4, and a piece with one stud — 1/8.
- When a long piece with 4 studs acts as a whole, a piece with 2 studs will be 1/2 , while a piece with one stud will be 1/4 .
- If you have a long piece with 3 studs as a whole, 2/3 will symbolize a piece with 2 studs, while 1/3 — a piece with one stud.
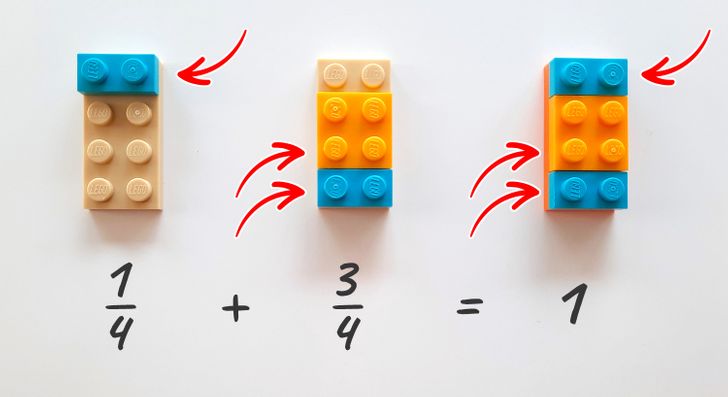
In a similar way, you can explain simple operations with fractions that have the same or a common denominator. In the picture above, we added 1/4 and 3/4, resulting in the whole. Using different colors helps to show how much of the whole each part takes up as a result of addition.
Assignment: Using Lego pieces as in the example above, try to add and subtract fractions with a common denominator with your child.
Method № 2: Dividing a circle into parts
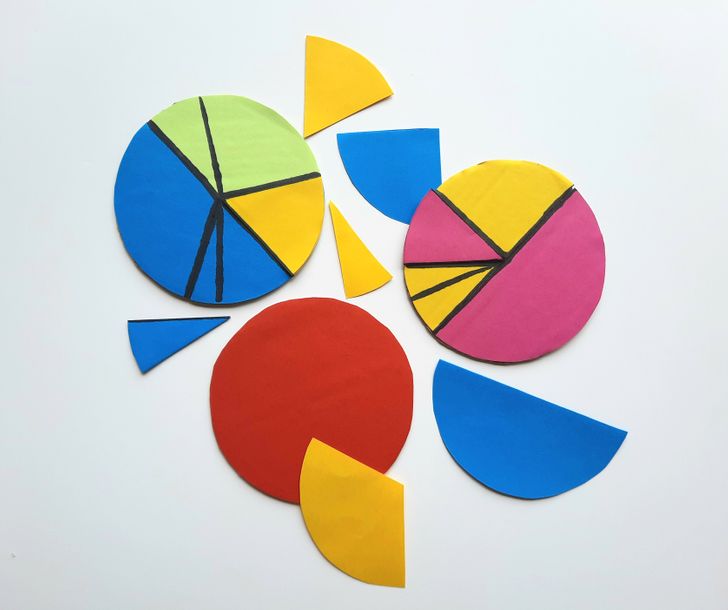
A fraction can be represented as a part of a whole. Understanding what this or that part looks like will help the child not only share a pizza or other round-shaped sweet treats with friends but also tell time on a regular clock face, e.g. it will be easier to explain what a quarter of an hour is.
To explain the division into parts, cut 3 identical circles out of cardboard.
- Cover the first circle completely with colored paper of the same color. It will symbolize the whole.

- Divide the second circle into 2 halves by drawing a line with an ordinary pencil. Cover one half with colored paper. Cover the other half with paper in a contrasting color, and then divide it in half again to get 2 quarters. Divide one of the quarters in half again, getting 2 eighths. Cover one of these 8 parts with colored paper. As a result, you got a circle divided into one half, one quarter, and 2 eighths.
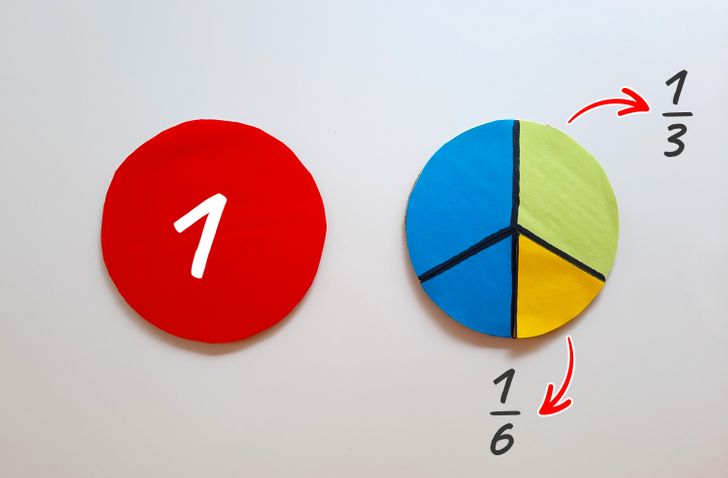
- Now divide the third circle into 3 equal parts. Cover one third with colored paper. Then divide the other third in half to get 2 parts equal to 1/6 of the circle. Cover one of them with a paper in a contrasting color. So, you will have half of the circle, which you can also glue with colored paper. In this way, you will be able to demonstrate 1/3 and 1/6 and show how they form 1/2 of a whole circle when added.

In addition, you can cut out separate parts from colored paper in order to put them on the whole (the very first circle) and thus, clearly show their meaning, as well as perform simple operations of addition and subtraction inside the circle.
Assignment: Try to assemble a whole circle with your child using different combinations of its parts.
Method № 3: Filling in the scale

An integer can be represented as a scale, where fractions are scale divisions. Using a marker and a ruler, draw a 12-division scale on a large sheet of paper like shown in the picture above. Each division is 2 cm long. Now take moldable clay or playdough and roll it into small balls that are about the size of cherries.

Invite your child to take one ball and put it in one of the small parts. To fill the entire scale, you’ll need 12 of these balls, but as you’ve probably noticed there is only one ball. Thus, you have 1/12 of the whole.

Now let’s add another ball to the scale. You can put it next to the first one or even glue it to make a pair. If you take 6 of these pairs, the entire scale will be filled. But there is only one of 6 or 1/6 of the whole. One more conclusion can be drawn from this:
- 1/6 = 1/12 +1/12

Now let’s add another ball. To fill the entire scale, you’ll only need 4 of these trios of balls. So far there is only a quarter, or 1/4 of the total required quantity to fill the scale.
The picture above shows:
- 1/4 = 1/12 +1/12 +1/12
- 1/4 = 1/6 +1/12
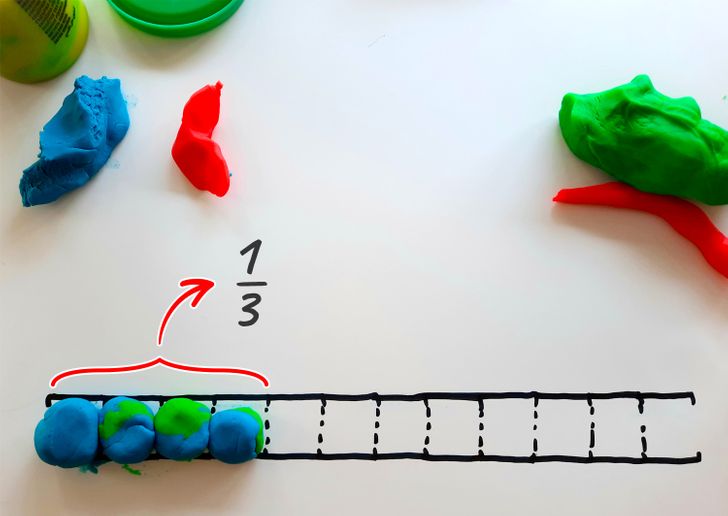
Let’s add another ball to fill 4 divisions at once. You’ll need 3 of these groups to fill the entire scale. There is only one out of 3 or 1/3 and you definitely remember that one division meant 1/12 and 2 divisions —1/6, so you’ll get:
- 1/3 = 1/12 +1/12 +1/12 +1/12
- 1/3 = 1/6 + 1/6
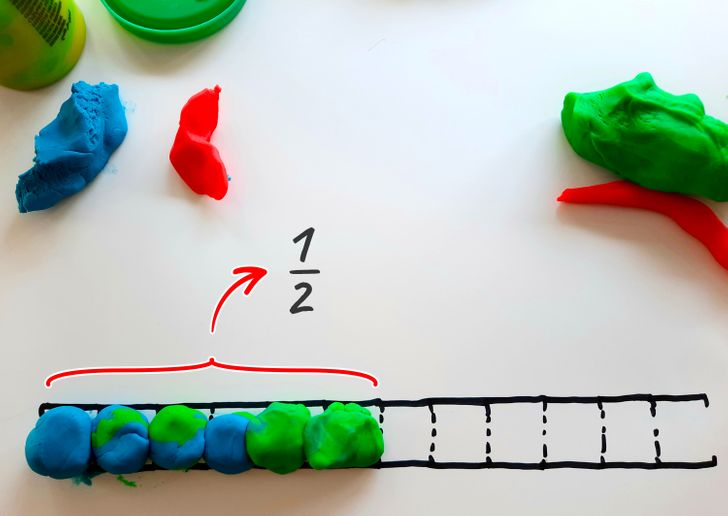
Now let’s add 2 balls to the scale so that we end up with 6. You filled in half of the divisions or 1/2. It can be concluded that:
- 1/2 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 1/2 = 1/6 + 1/6 + 1/6
- 1/2 = 1/3 +1/6
- 1/2 = 1/4 +1/4
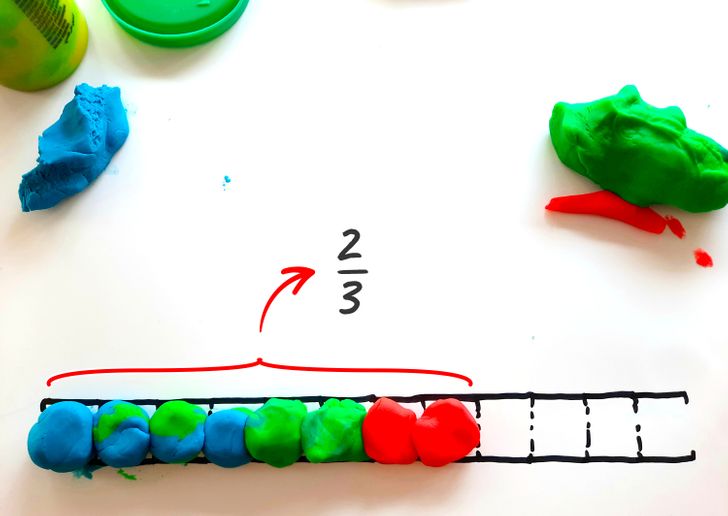
Add a couple more balls to make it 8. So, you filled in 2/3 of the whole scale. What are 2 thirds made of?
- 2/3 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 2/3 = 1/6 + 1/6 + 1/6 + 1/6
- 2/3 = 1/3 +1/3
- 2/3 = 1/4 + 1/4 + 1/6
- 2/3 = 1/2 + 1/6

Let’s fill in one more division with a ball to cover 9 cells. This is 3 quarters of the entire scale. It can be represented in the following way:
- 3/4 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 3/4 = 1/6 + 1/6 + 1/6 + 1/6 +1/12
- 3/4 = 1/3 +1/3 +1/12
- 3/4 = 1/2 + 1/6 +1/12

Finally, if you add 3 more balls, you’ll fill the entire scale, getting an integer.
Method № 4: Indicating ratio

Draw 7 tiny figures. Let them differ by color of clothing and hair, in posture, and in the presence of certain objects. In this case, you can consider a group of tiny figures as a whole.

2 out of 7 figures (2/7) have a balloon in their hands, and 5 out of 7 (5/7) don’t have any. Here the fraction does not just divide the whole, but it helps to indicate the ratio.
So, everything can be divided. As an alternative example, consider a mug of hot chocolate:
☕ = ?? / ???
which consists of 2/5 of delicious chocolate and 3/5 of fresh milk.
What are decimals?

Take a piece of paper and draw a 100-cell square table on it. It is considered to be a whole that is divided into 100 identical parts or cells.
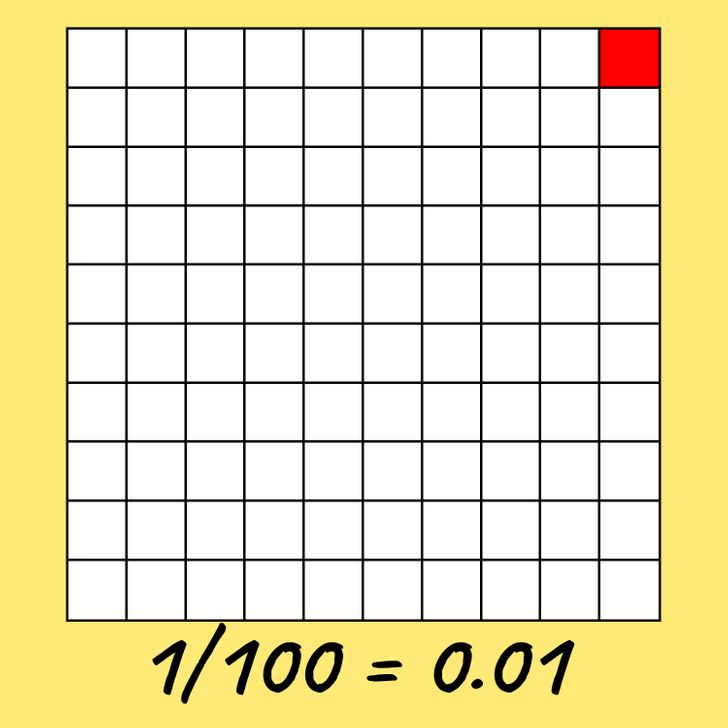
Now color in one cell. This is one of the 100 parts of the table. In the form of an ordinary fraction, it will look like 1/100. It can also be written in a line with a period to separate the integer part from the fractional one:
1/100 = 0.01
The number written to the left of the decimal is the integer, while the part from the decimal to the right are tenths, hundredths, thousandths, ten-thousandths, and smaller, but always multiples of 10. In other words, if the denominator of a simple fraction equals 10, 100, 1,000, 10,000, and the like, we have a decimal fraction. This simplifies the form of the fraction, for example:
- 0.8 = 8/10
- 14.89 = 1,489/100
- 3.14 159 = 314,159/100 000
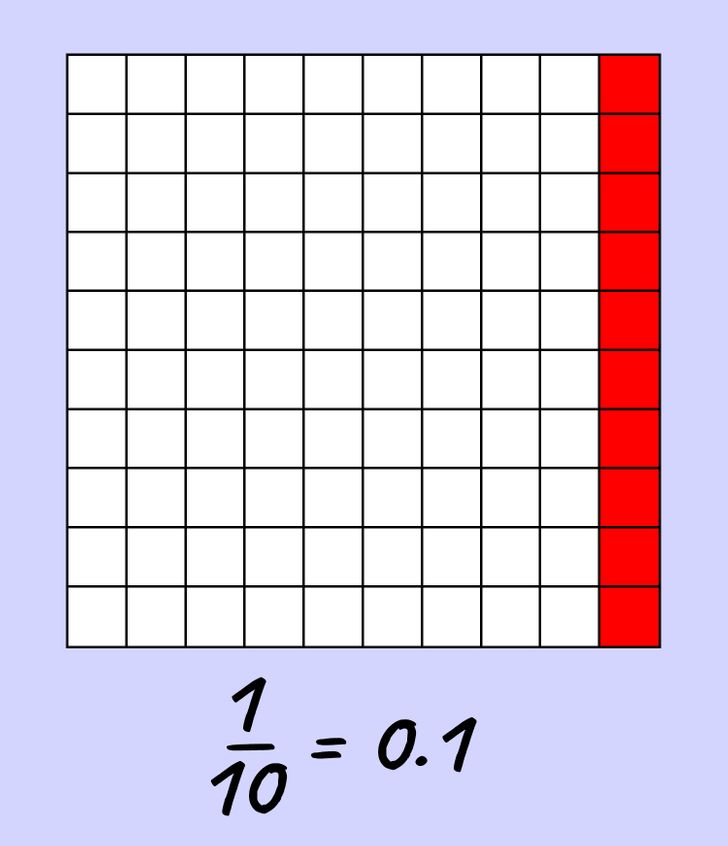
Now let’s fill in all columns in the table. The entire table consists of 10 columns, so it means that one column is equal to one-tenth of the table.
Here you can use 0.1 instead of 1/10.
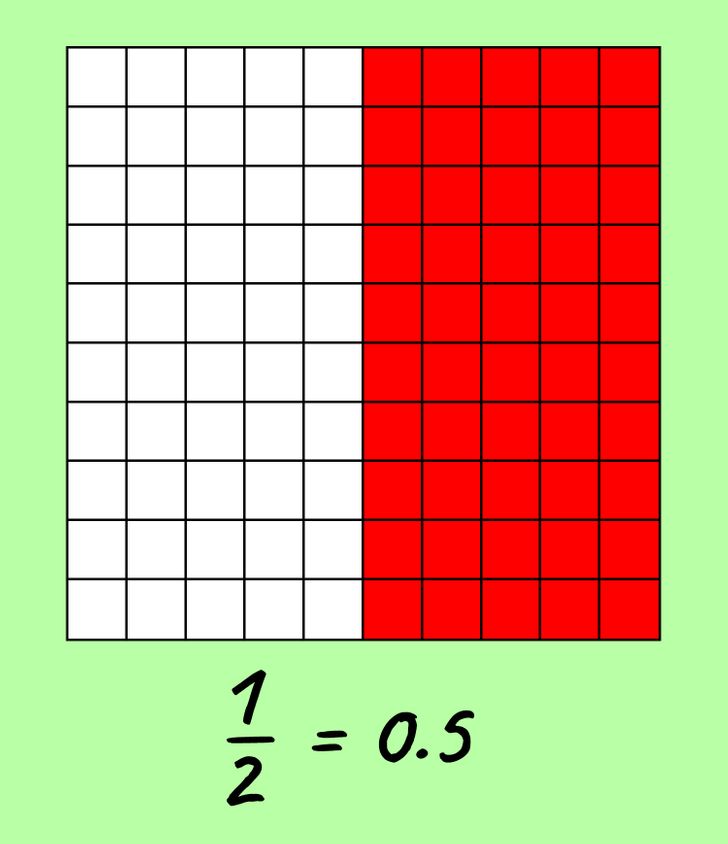
If you fill in 4 more columns, it means you have painted over five-tenths, or 0.5. The picture above shows that this is exactly half or 1/2 of the table.
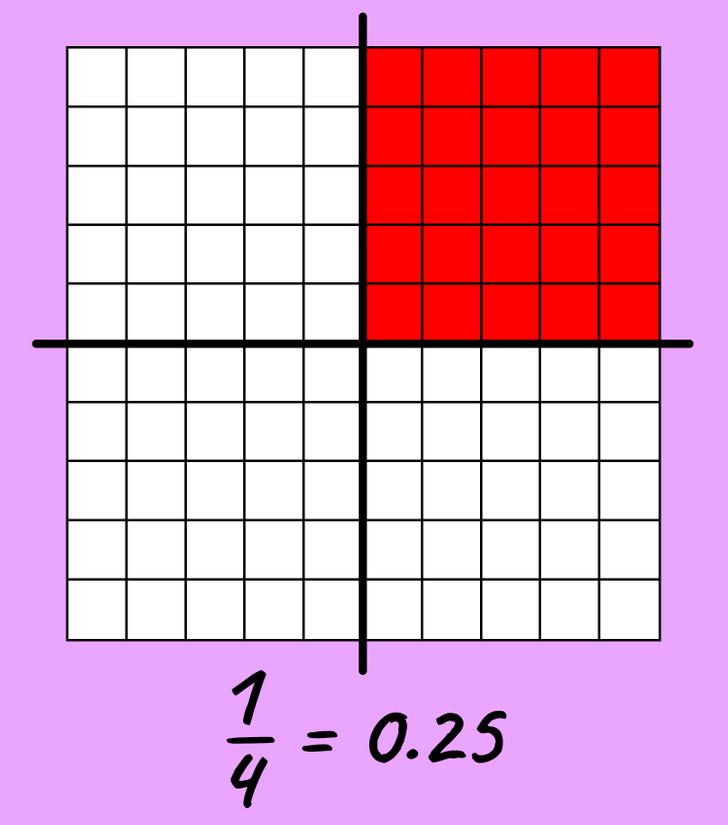
Let’s say that you took an empty table again and divided it into 4 equal parts. One part was painted over: there turned out to be 25 cells out of 100, or 0.25. Thus, we see that 1/4 = 0.25.
So, same numbers can be written in the form of ordinary and decimal fractions:
- 3/4 = 0.75
- 1/2 = 0.5
- 1/4 = 0.25
- 1/5 = 0.2
- 1/10 = 0.1
- 1/100 = 0.01
Assignment: Draw several empty square tables of 100 cells and tell your child to paint over the cells, which represent different decimals and ordinary fractions, and compare them with each other. This will help them visually see and remember that, for example, 3/4 is more than 0.3 or 0.4.
5-Minute Crafts gets commissions for purchases made through links in this post.