How To Find the Square Root of Any Number
Many people think math is hard and finding answers to some equations can seem impossible, especially if you are trying to solve square roots. But, did you know that this operation can actually be very easy? Using some interesting tricks you can turn these calculations into a fun activity and solving these problems will no longer be such an issue.
5-Minute Crafts will show you a few easy steps for how to quickly find the square root of any number.
1. Check your knowledge about perfect squares.

The first step is to have a working knowledge of the perfect squares. These numbers, from a given system, are obtained by squaring a whole digit or an integer. A perfect square is, for example, number 25, because it is the product of integer 5 by itself — 5×5 = 25.
Most people memorize the square roots of integers so they can quickly solve equations.
Now let’s see what do to if you don’t have a figure with a perfect square in front of you.
2. First look for the closest perfect square below the number.

- We took, for example, the number 87.
- The closest perfect square to 87 is 81.
3. Find the root number now.

- In this case, the root number of 81 is 9.
4. Calculate the difference between the square number and the example you are trying to solve.
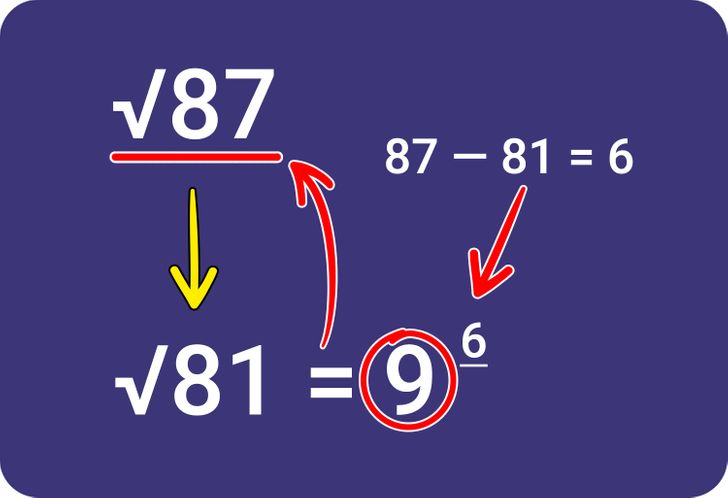
- Subtract 87 and 81.
- When you get the difference (6), write it next to the number 9.
5. Double the whole number square.
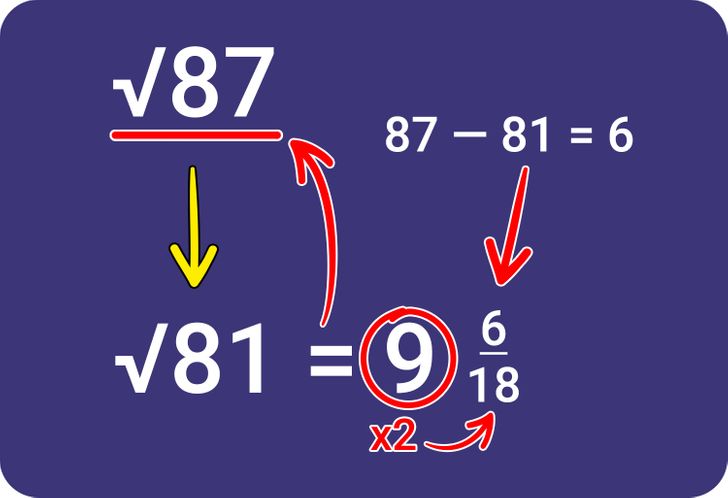
- Double the number 9 and write it next to it, under the number 6, making it into a fraction.
6. Divide the fraction next to the whole square number.
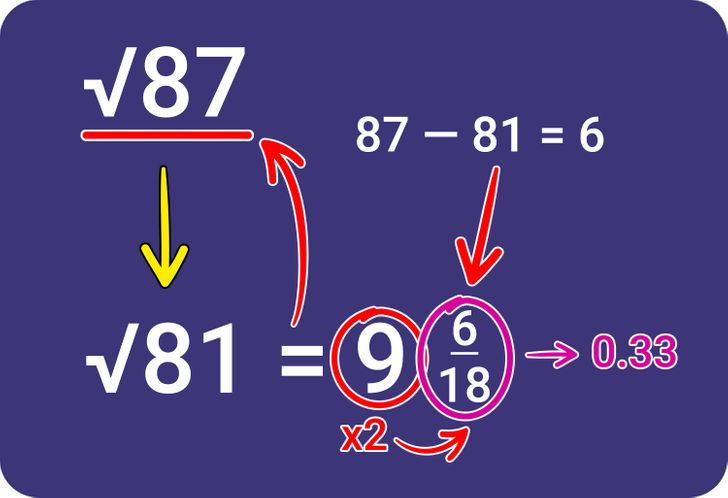
- Divide the fraction that is next to the whole number.
- In this case, 6 / 18 equals 0.33.
7. Write down the result that you got.
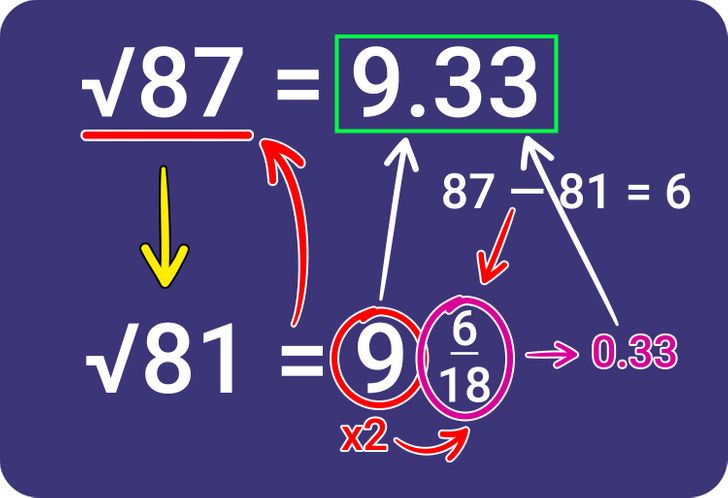
- The whole number square 9 and the result of the fraction (0.33) are together the result of the square root of 87.
Note: This trick can help you to find the answer quickly and also help you practice your equation-solving skills. But bear in mind that the answer isn’t completely accurate — it is rounded up. So, for example, we found our answer for the square root of 87 which is 9.33 but the precise result is 9.327.